Cours de La Recherche Opérationnelle
COURS DE LA RECHERCHE OPÉRATIONNELLE
Cours Recherche Opérationnelle
Chapitre 1 : Formulation d’un programme linéaire (PL)I. Introduction
II. Les conditions de formulation d’un PL
III. Les étapes de formulation d’un PL
IV. Présentation Théorique
V. Exemples de formulations
Chapitre 2 : Résolution d’un programme linéaire (PL)
I. Introduction
II. Système d’axes
III. Représentation graphique des contraintes
IV. Représentation de la fonction objectif
V. Recherche de la solution optimale
a. Résolution graphique
b. Résolution par énumération :
VI. Exemples
VII. Analyse de sensibilité
Chapitre 3 :La Méthode de Simplexe
I. Introduction
II. Mise sous forme standard
III. Revue algébrique de la méthode du simplexe
IV. La méthode des tableaux
a. Tableau de simplexe initial
b. Amélioration de la solution
c. Calcul des tableaux suivants
V. Résumé de la procédure de la méthode du simplexe
VI. Exemple
Chapitre 4 : Problèmes de Minimisation et Problèmes Irréguliers
I. Introduction
II. Les variables artificielles
III. Les problèmes de minimisation
IV. Les problèmes irréguliers
a. Les problèmes impossibles
b. Les problèmes à solutions multiples
c. Les problèmes à solution infinie
d. Les problèmes à solution dégénérée
Chapitre 5 : Dualité et analyse de sensibilité
I. Introduction
II. Interprétation économique
III. Dualité
a. Définition
b. Propriétés et signification économique du programme dual
c. Tableau de correspondance primal-dual
III. Analyse de sensibilité
a. Analyse de sensibilité sur les Cj
b. Analyse de sensibilité sur les bj
c. Analyse de sensibilité sur les coefficients aij
IV. Introduction d’une nouvelle activité
a. Introduction d’une nouvelle variable de décision
b. Introduction d’une nouvelle contrainte
Chapitre 6 : Introduction à la Programmation Dynamique
I. Introduction
II. Exemple prototype. Le problème du voyageur
III. Caractéristiques d’un problème de programmation dynamique
IV. Programmation dynamique déterministe
a. Introduction
b. Problème du type plus court chemin
c. Répartition optimale des moyens
d. Résolution d'un programme linéaire
CHAPITRE 1
Formulation d’un programme linéaire (PL)
I. Introduction
L’importance de l’optimisation et la nécessité d’un outil simple pour modéliser des problèmes de décision que soit économique, militaire ou autres on fait de la programmation linéaire un des champs de recherche les plus actifs au milieu du siècle précédent. Les premiers travaux (1947) sont celle de George B. Dantzig et ses associés du département des forces de l’air des Etats Unis d’Amérique.
Les problèmes de programmations linéaires sont généralement liés à des problèmes d’allocations de ressources limitées, de la meilleure façon possible, afin de maximiser un profit ou de minimiser un coût. Le terme meilleur fait référence à la possibilité d’avoir un ensemble de décisions possibles qui réalisent la même satisfaction ou le même profit. Ces décisions sont en général le résultat d’un problème mathématique.
II. Les Conditions de formulation
La programmation linéaire comme étant un modèle admet des hypothèses (des conditions) que le décideur doit valider avant de pouvoir les utiliser pour modéliser son problème. Ces hypothèses sont :
- Les variables de décision du problème sont positives
- Le critère de sélection de la meilleure décision est décrit par une fonction linéaire de ces variables, c’est à dire, que la fonction ne peut pas contenir par exemple un produit croisé de deux de ces variables. La fonction qui représente le critère de sélection est dite fonction objectif (ou fonction économique).
- Les restrictions relatives aux variables de décision (exemple: limitations des ressources) peuvent être exprimées par un ensemble d’équations linéaires. Ces équations forment l’ensemble des contraintes.
- Les paramètres du problème en dehors des variables de décisions ont une valeur connue avec certitude
III. Les étapes de formulation d’un PL :
Généralement il y a trois étapes à suivre pour pouvoir construire le modèle d'un programme linéaire :
- Identifier les variables du problème à valeur non connues (variable de décision) et les représenter sous forme symbolique (exp. x1, y1 ).
- Identifier les restrictions (les contraintes) du problème et les exprimer par un système d’équations linéaires.
- Identifier l’objectif ou le critère de sélection et le représenter sous une forme linéaire en fonction des variables de décision. Spécifier si le critère de sélection est à maximiser ou à minimiser.
IV. Présentation Théorique
Un programme linéaire consiste à trouver le maximum ou le minimum d’une forme linéaire dite fonction objectif en satisfaisant certaines équations et inégalités dites contraintes. En langage mathématique, on décrira de tels modèles de la manière suivante :
Soient N variables de décision x1, x2,…, xn, l’hypothèse que les variables de décision sont positives implique que
La fonction objectif est une forme linéaire en fonction des variables de décision de type
où les coefficients c1,…,cN doivent avoir une valeur bien déterminée (avec certitude) et peuvent être positifs, négatifs ou nuls. Par exemple le coefficient ci peut représenter un profit unitaire lié à la production d’une unité supplémentaire du bien xi, ainsi la valeur de z est le profit total lié à la production des différents biens en quantités égales à 
Supposons que ces variables de décision doivent vérifier un système d’équations linéaires définis par M inégalités
où les coefficients a1M,…, aMN et b1,…, bM doivent avoir une valeur bien déterminée (avec certitude) et peuvent être positifs, négatifs ou nuls. Le paramètre bj représente la quantité de matière première disponible dont le bien xi utilise une quantité égale à aij xi .
En suivant les étapes de formulation ci-dessus, on peut représenter le PL comme suit :
V. Exemples de formulations
Limité au départ aux problèmes industriels et militaires, de nos jours plusieurs problèmes de divers domaines sont représentés ou approximés par des modèles de PL. L’utilisation de ces techniques de modélisation s’est renforcée encore après avoir construit des algorithmes et des logiciels capables de résoudre de plus larges problèmes avec autant de variables de décision que de contraintes.
La tâche de formulation demande généralement une certaine expertise et connaissance du problème pour pouvoir relever facilement les différentes composantes du problème et ainsi donner un programme qui modélise au mieux la situation réelle. Dans ce qui suit, on présentera quelques exemples de formulation en programme linéaire liés à différents problèmes de décision :
Exemple 1 : Problème d’agriculture
Un agriculteur veut allouer 150 hectares de surface irrigable entre culture de tomates et celles de piments. Il dispose de 480 heures de main d’œuvre et de 440 m3 d’eau. Un hectare de tomates demande 1 heure de main d’œuvre, 4 m3 d’eau et donne un bénéfice net de 100 dinars. Un hectare de piments demande 4 heures de main d’œuvre, 2 m3 d’eau et donne un bénéfice net de 200 dinars.
Le bureau du périmètre irrigué veut protéger le prix des tomates et ne lui permet pas de cultiver plus de 90 hectares de tomates. Quelle est la meilleure allocation de ses ressources ?
Formulation du problème en un PL :
Etape 1 : Identification des variables de décision. Les deux activités que l’agriculteur doit déterminer sont les surfaces à allouer pour la culture de tomates et de piments :
- x1 : la surface allouée à la culture des tomates
- x2 : la surface allouée à la culture des piments
On vérifie bien que les variables de décision x1 et x2 sont positives :  .
.
Etape 2 : Identification des contraintes. Dans ce problème les contraintes représentent la disponibilité des facteurs de production :
- Terrain : l’agriculteur dispose de 150 hectares de terrain, ainsi la contrainte liée à la limitation de la surface de terrain est
- Eau : la culture d’un hectare de tomates demande 4 m3 d’eau et celle d’un hectare de piments demande 2m3 mais l’agriculteur ne dispose que de 440m3. La contrainte qui exprime les limitations des ressources en eau est
.
- Main d’œuvre : Les 480 heures de main d’œuvre seront départager (pas nécessairement en totalité) ente la culture des tomates et celles des piments. Sachant qu’un hectare de tomates demande une heure de main d’œuvre et un hectare de piments demande 4 heures de main d’œuvre alors la contrainte représentant les limitations des ressources humaines est
- Les limitations du bureau du périmètre irrigué : Ces limitations exigent que l’agriculteur ne cultive pas plus de 90 hectares de tomates. La contrainte qui représente cette restriction est
Etape 3 : Identification de la fonction objectif. La fonction objectif consiste à maximiser le profit apporté par la culture de tomates et de piments. Les contributions respectives 100 et 200, des deux variables de décision x1 et x2 sont proportionnelles à leur valeur. La fonction objectif est donc 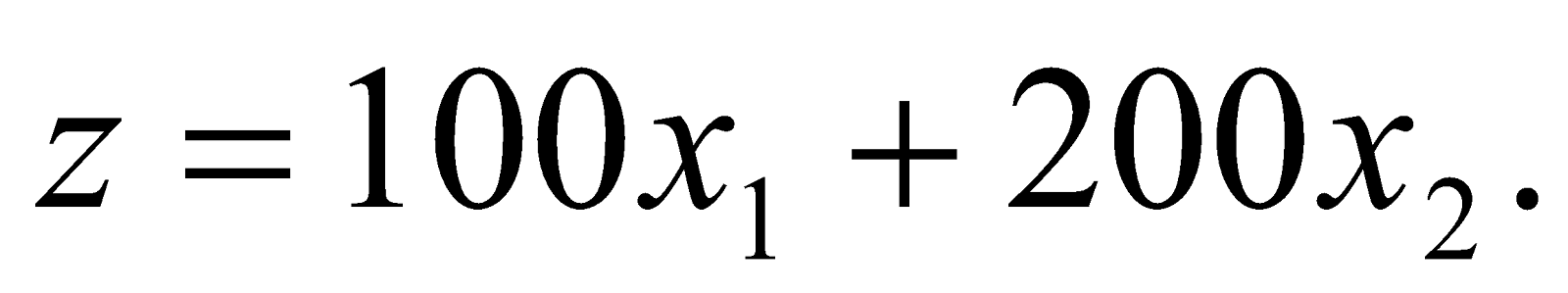
Le programme linéaire qui modélise le problème d’agriculture est :
Exemple 2 : Problème de médecine
Un spécialiste en médecine a fabriqué un médicament (des pilules) pour guérir les sujets atteints d’un rhume. Ces pilules sont fabriquées selon deux formats :
- Petite taille : elle contient 2 grains d’aspirine, 5 grains de bicarbonate et 1 grain de codéine.
- Grande taille : elle contient 1 grain d’aspirine, 8 grains de bicarbonate et 6 grains de codéine.
Pour guérir la maladie, le sujet a besoin de 12 grains d’aspirine, 74 grains de bicarbonate et 24 grains de codéine. Déterminer le nombre de pilules minimales à prescrire au sujet pour qu’il soit guérit.
Formulation du problème en un PL :
Le problème de médecine présente certaines ressemblances avec le problème de l’agriculture, dans les deux cas c’est un problème d’allocation de ressources.
Les variables de décision qui représentent des valeurs inconnues par le décideur qui est dans ce cas le spécialiste en médecine sont :
- x1 : le nombre de pilules de petite taille à prescrire.
- x2 : le nombre de pilules de grande taille à prescrire.
On vérifie bien que les variables de décision x1 et x2 sont positives :  .
.
Les contraintes imposées par le problème sur les valeurs possibles de x1 et x2 sont :
- La prescription doit contenir des pilules avec au moins 12 grains d’aspirine. Sachant qu’une petite pilule contient 2 grains d’aspirine et qu’une grande pilule contient un seul grain d’aspirine, on obtient la contrainte suivante :
.
- De la même façon que pour l’aspirine, la prescription du spécialiste en médecine doit contenir au moins 74 grains de bicarbonate. Ainsi la contrainte suivante doit être satisfaite :
.
- Finalement la contrainte imposée par le fait que la prescription doit contenir au moins 24 grains de codéine est
.
Etape 3 : Identification de la fonction objectif. On remarque qu’il y a plusieurs couples de solutions  qui peuvent satisfaire les contraintes spécifiées à l’étape 2. La prescription doit contenir le minimum possible de pilules. Donc le critère de sélection de la quantité de pilules à prescrire est celle qui minimise le nombre total des pilules
qui peuvent satisfaire les contraintes spécifiées à l’étape 2. La prescription doit contenir le minimum possible de pilules. Donc le critère de sélection de la quantité de pilules à prescrire est celle qui minimise le nombre total des pilules 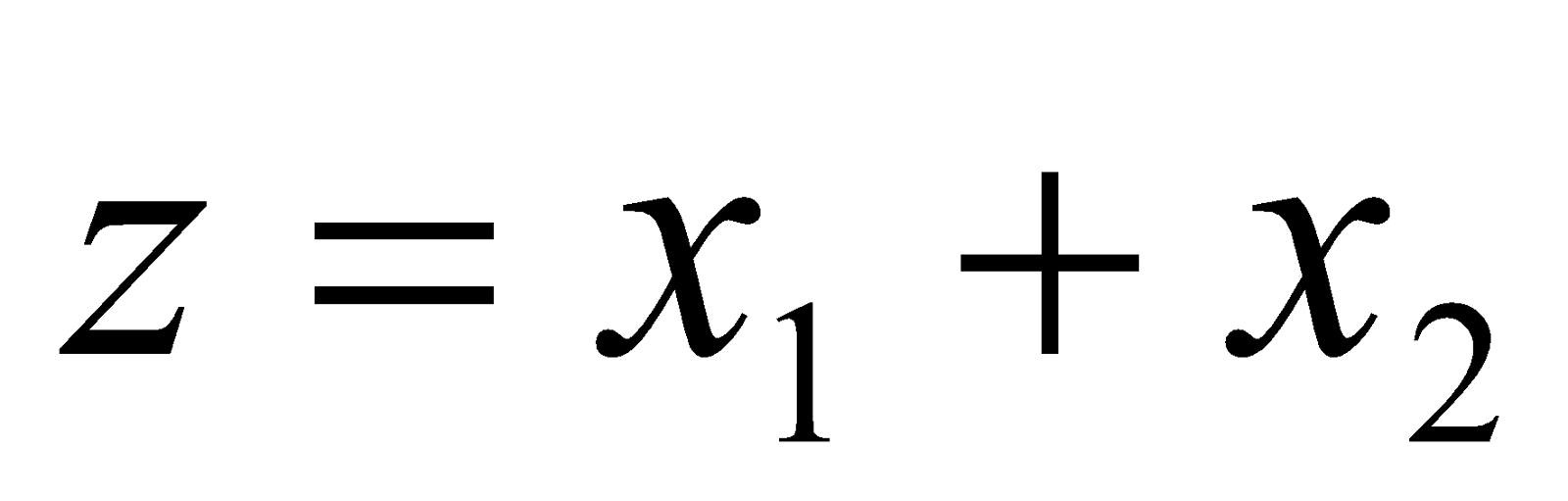 .
.
Le programme linéaire qui modélise ce problème médical est donc le suivant :
Exemple 3 : problème de production
Pour fabriquer deux produits P1 et P2 on doit effectuer des opérations sur trois machines M1, M2 et M3, successivement mais dans un ordre quelconque. Les temps unitaires d’exécution sont donnés par le tableau suivant :
M1
|
M2
|
M3
| |
P1
|
11 mn
|
7 mn
|
6 mn
|
P2
|
9 mn
|
12 mn
|
16 mn
|
On supposera que les machines n’ont pas de temps d’inactivité.
La disponibilité pour chaque machine sont :
- 165 heures (9900 minutes) pour la machine M1 ;
- 140 heures (8400 minutes) pour la machine M2 ;
- 160 heures (9600 minutes) pour la machine M3 .
Le produit P1 donne un profit unitaire de 900 dinars et le produit P2 un profit unitaire de 1000 dinars.
Dans ces conditions, combien doit-on fabriquer mensuellement de produits P1 et P2 pour avoir un profit total maximum ?
Formulation en un PL :
Les variables de décisions sont :
- x1 : le nombre d’unités du produit P1 à fabriquer
- x2 : le nombre d’unités du produit P2 à fabriquer
Les contraintes outre les contraintes de non-négativité sont :
pour la machine M1
pour la machine M2
pour la machine M3
Le profit à maximiser est : 
Le programme linéaire résultant est :
Exemple 4 : Problème d’alimentation
On se propose de réaliser une alimentation économique pour des bestiaux, qui contient obligatoirement 4 sortes de composants nutritifs, A, B, C et D. L’industrie alimentaire produit précisément deux aliments M et N qui contiennent ces composants : 1 Kg d’aliment M contient 100 g de A, 100 g de C, 200 g de D ; 1 Kg d’aliment N contient 100 g de B, 200 g de C, 100 g de D.
Un animal doit consommer par jour au moins : 0.4 Kg de A ; 0.6 Kg de B ; 2 Kg de C ; 1.7 Kg de D. L’aliment M coûte 10 DT le Kg et N coûte 4 DT le Kg. Quelles quantités d’aliments M et N doit-on utiliser par jour et par animal pour réaliser l’alimentation la moins coûteuse ?
Formulation en un PL :
On peut résumer toutes les données du problème dans le tableau suivant
M
|
N
|
Quantités prescrites
| |
A
|
0.1
|
0
|
0.4
|
B
|
0
|
0.1
|
0.6
|
C
|
0.1
|
0.2
|
2
|
D
|
0.2
|
0.1
|
1.7
|
Coût
|
10
|
4
|
Ce genre de tableau peut aider à mieux analyser le problème et ainsi formuler le programme linéaire correspondant.
Les variables de décision sont
- xM : la quantité d’aliments M à utiliser pour l’alimentation des deux bestiaux
- xN : la quantité d’aliments N à utiliser pour l’alimentation des deux bestiaux
Les contraintes de non-négativité sont 
Le choix de cette quantité est contraint à la présence dans l’alimentation du composant
- A :
- B :
- C :
- D :
La fonction objectif est une fonction coût :  .
.
Le programme linéaire est un programme de minimisation :
Exemple 5 : Problème de mélange
Un industriel veut produire un alliage Z à 30% de plomb, 30% de zinc et 40% d’étain. Supposons qu’il puisse se procurer sur le marché des alliages A, B, C, D, E, F, G, H, I dont les compositions et les prix respectifs sont donnés dans le tableau suivant :
Compositions des alliages
(en %) |
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
Alliage à fabriquer
|
Plomb
|
10
|
10
|
40
|
60
|
30
|
30
|
30
|
50
|
20
|
30
|
Zinc
|
10
|
30
|
50
|
30
|
30
|
40
|
20
|
40
|
30
|
30
|
Etain
|
80
|
60
|
10
|
10
|
40
|
30
|
50
|
10
|
50
|
40
|
Coût au Kilo
|
4.1
|
4.3
|
5.8
|
6
|
7.6
|
7.5
|
7.3
|
6.9
|
7.3
|
Combien doit-il acheter de chaque alliages A, B, C, D, E, F, G, H et I pour obtenir au prix de revient minimum un 1 Kg de l’alliage Z ?
Formulation en un PL :
La décision à prendre : Combien acheter de chaque alliage A, B, …, I ?
Les variables de décision sont :
- xi : la quantité d’alliage i, i= A, B, …, I, à acheter.
On vérifie bien que les variables de décision xi , i= A, B, …, I, sont positives : 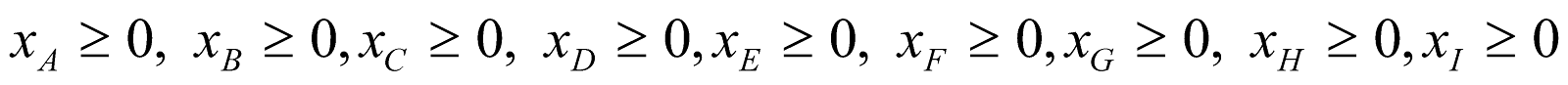 .
.
Les contraintes relatives au problème sont :
- Equation de la conservation de la matière :
- Equation de la satisfaction des proportions en Plomb :
- Equation de la satisfaction des proportions en Zinc :
- Equation de la satisfaction des proportions en Etain :
La fonction objectif dans cet exemple représente le coût d’achat des différents alliages A, B, C, D, E, F, G, H et I. Donc l’expression de la fonction objectif est la suivante :
Le programme linéaire qui modélise ce problème mélange s'écrit :
Exemple 6 : Sélection de Médias
Une entreprise désire effectuer une campagne publicitaire dans la télévision, la radio et les journaux pour un produit lancé récemment sur le marché. Le but de la campagne est d’attirer le maximum possible de clients. Les résultats d’une étude de marché sont donnés par le tableau suivant :
Télévision
|
Radio
|
Journaux
| ||
Locale
|
Par satellite
| |||
Coût d’une publicité
|
40 DT
|
75 DT
|
30 DT
|
15 DT
|
Nombre de client potentiel par publicité
|
400
|
900
|
500
|
200
|
Nombre de client potentiel femme par publicité
|
300
|
400
|
200
|
100
|
Pour la campagne, on prévoit de ne pas payer plus que 800DT pour toute la campagne et on demande que ces objectifs soient atteints :
- Au minimum 2000 femmes regardent, entendent ou lisent la publicité ;
- La campagne publicitaire dans la télévision ne doit pas dépasser
500 DT ; - Au moins 3 spots publicitaires seront assurer par la télévision locale et au moins de deux spots par la télévision par satellite.
- Le nombre des publicités dans la radio ou dans les journaux sont pour chacun entre 5 et 10.
Formulation en un PL :
Les variables de décision du problème sont
- x1 : le nombre de spots publicitaires dans la télévision locale
- x2 : le nombre de spots publicitaires dans la télévision par satellite
- x3 : le nombre de spots publicitaires dans la radio
- x4 : le nombre d’affiches publicitaires dans les journaux
Les contraintes de non-négativité sont vérifiées.
Les contraintes du problème sont :
- Coût total de la compagne publicitaire :
- Nombre de clients femmes potentiels par publicité :
- Contraintes de la télévision :
,
et
- Contraintes sur le nombre de publicités dans la radio et dans les journaux
et
.
La fonction objectif à maximiser représente le nombre de clients potentiels par publicité  .
.
Le programme linéaire résultant est :
Excellent...
RépondreSupprimer