La Méthode de Simplexe - Cours de La Recherche Opérationnelle



COURS DE LA RECHERCHE OPÉRATIONNELLE


Cours  Recherche Opérationnelle

Chapitre 1 : Formulation d’un programme linéaire (PL)
I. Introduction
II. Les conditions de formulation d’un PL
III. Les étapes de formulation d’un PL
IV. Présentation Théorique
V. Exemples de formulations

Chapitre 2 : Résolution d’un programme linéaire (PL)
I. Introduction
II. Système d’axes
III. Représentation graphique des contraintes
IV. Représentation de la fonction objectif
V. Recherche de la solution optimale
a. Résolution graphique
b. Résolution par énumération :
VI. Exemples
VII. Analyse de sensibilité

Chapitre 3 :La Méthode de Simplexe
I. Introduction
II. Mise sous forme standard
III. Revue algébrique de la méthode du simplexe
IV. La méthode des tableaux
a. Tableau de simplexe initial
b. Amélioration de la solution
c. Calcul des tableaux suivants
V. Résumé de la procédure de la méthode du simplexe
VI. Exemple

Chapitre 4 : Problèmes de Minimisation et Problèmes Irréguliers
I. Introduction
II. Les variables artificielles
III. Les problèmes de minimisation
IV. Les problèmes irréguliers
a. Les problèmes impossibles
b. Les problèmes à solutions multiples
c. Les problèmes à solution infinie
d. Les problèmes à solution dégénérée

Chapitre 5 : Dualité et analyse de sensibilité
I. Introduction
II. Interprétation économique
III. Dualité
a. Définition
b. Propriétés et signification économique du programme dual
c. Tableau de correspondance primal-dual
III. Analyse de sensibilité
a. Analyse de sensibilité sur les Cj
b. Analyse de sensibilité sur les bj
c. Analyse de sensibilité sur les coefficients aij
IV. Introduction d’une nouvelle activité
a. Introduction d’une nouvelle variable de décision
b. Introduction d’une nouvelle contrainte

Chapitre 6 : Introduction à la Programmation Dynamique
I. Introduction
II. Exemple prototype. Le problème du voyageur
III. Caractéristiques d’un problème de programmation dynamique
IV. Programmation dynamique déterministe
a. Introduction
b. Problème du type plus court chemin
c. Répartition optimale des moyens
d. Résolution d'un programme linéaire

CHAPITRE 3

La Méthode de Simplexe


I. Introduction

On a présenté dans le chapitre précédent une procédure graphique pour résoudre un programme linéaire à deux variables. Par contre, dans la plupart des problèmes réels, on a plus que deux variables à déterminer. Une procédure algébrique pour résoudre les programmes linéaires avec plus que deux variables fera l’objet de ce chapitre. C'est la méthode de simplexe.

Une implémentation de cette procédure à permis de résoudre des programmes avec un peu plus de quelques milliers de variables. Le programme Lindo qu’on présentera dans le chapitre 7 (en version pour étudiant) supporte au plus 200 variables et 100 contraintes.

Dans ce chapitre la méthode de simplexe est présentée pour les problèmes 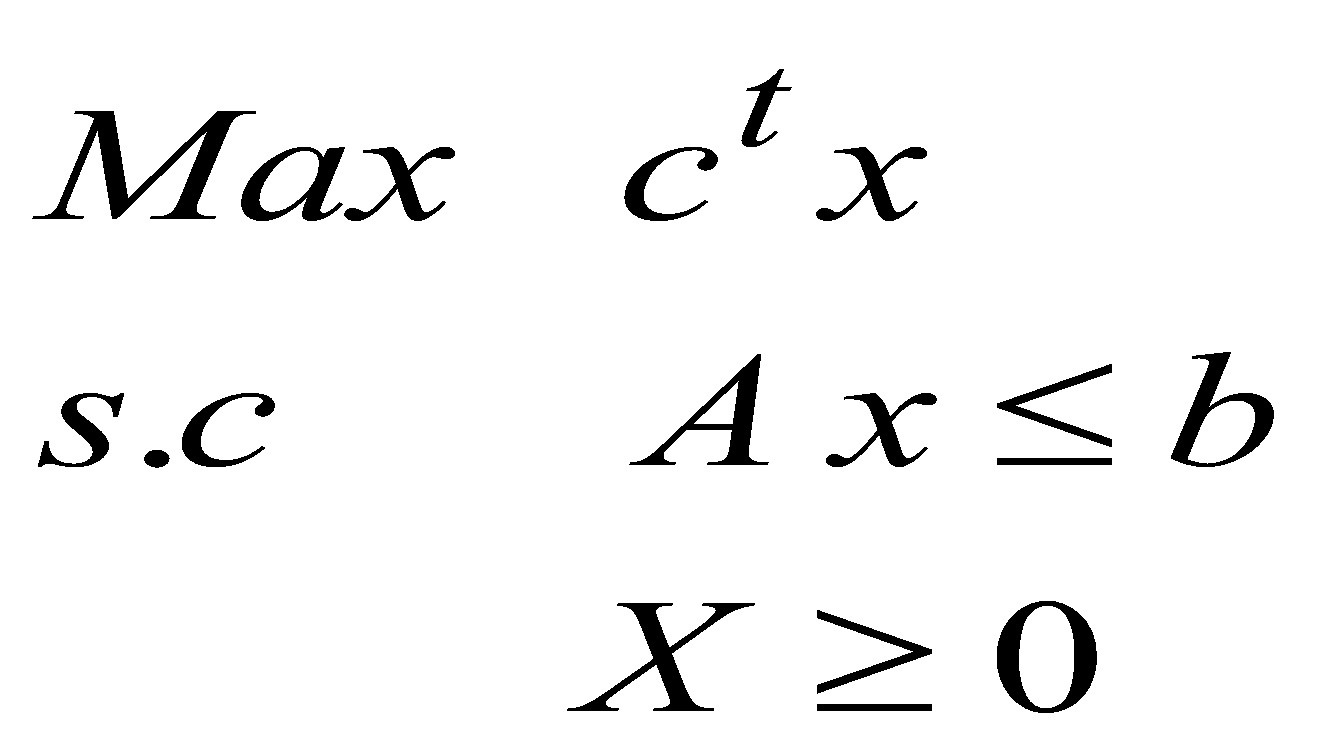et en utilisant le problème de l’agriculteur :

II. Mise sous forme standard

La mise sous forme standard consiste à introduire des variables supplémentaires (une pour chaque contrainte) de manière a réécrire les inégalités (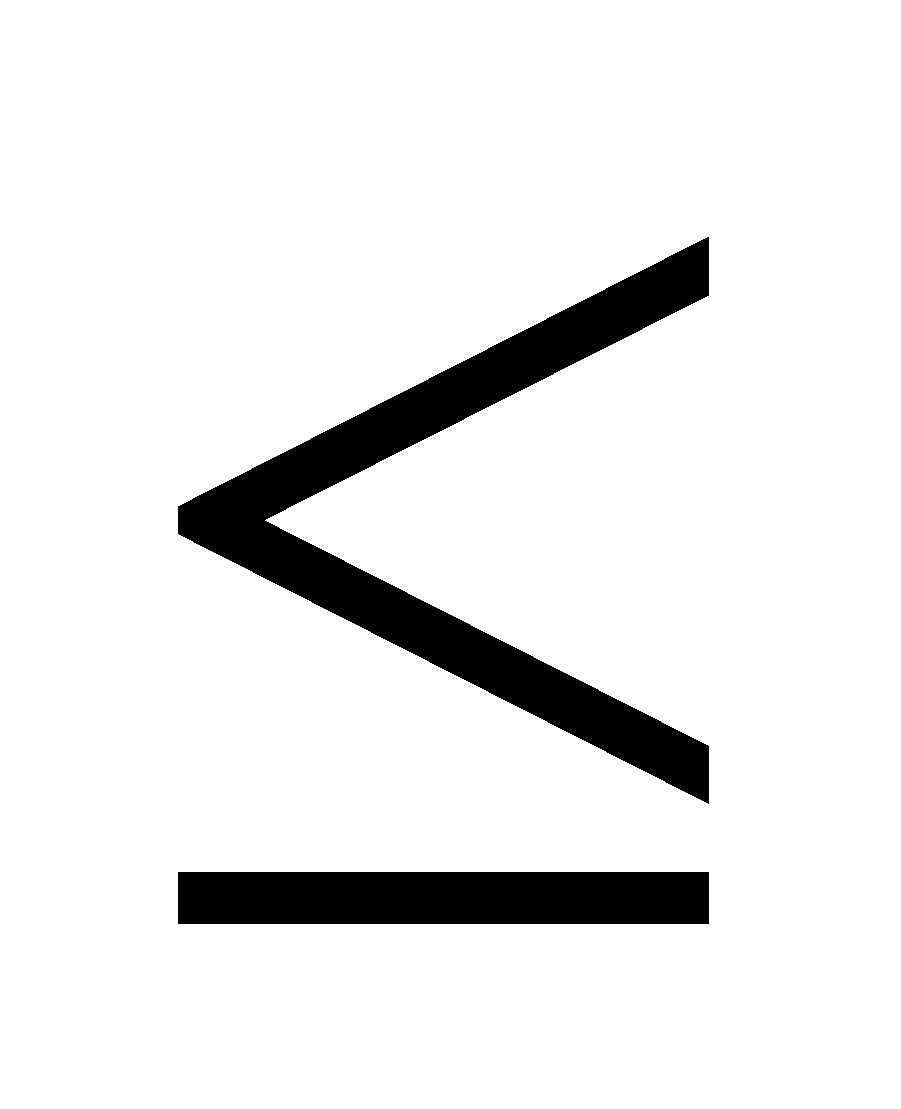) sous la forme d'égalités. Chacune de ces variables représente le nombre de ressources non utilisés. On les appelle variable d'écart. La forme standard s'écrit donc :
    ⇔   
La forme standard du programme linéaire de l'agriculteur est :
    Max    100x1 + 200x2            (3.1)
    s. c       x1 + x2 + S1 = 150        (3.2)
                         4x1 + 2x2 + S2 = 440    (3.3)
           x1 + 4x2 + S3 = 480    (3.4)
           x1 + S4 = 90        (3.5)
           x1, x2, S1, S2, S3, S4 ≥0    (3.6)
L'impact de ces variables d'écart sur la fonction objectif est nulle. Ceci explique le fait que leur existence soit tout simplement liée à une mise en forme du programme linéaire initial. Ces variables d'écart peuvent prendre des valeurs nonnegatives. Le fait de donner la valeur des variables d'écart a l'optimum donne une idée du nombre des ressources non utilisées.

III. Revue algébrique de la méthode du simplexe

La question qui se pose : que demande-t-on d’une procédure algébrique ?

En premier lieu, on note que les contraintes du problème (3.2)-(3.5), forment un système de 4 équations et de 6 variables. Or il y a un nombre infini de solutions de ce système d’équations. Donc une procédure algébrique, pour la résolution d’un programme linéaire doit être capable de retrouver les solutions des systèmes d’équations où il y a plus de variables que de contraintes.

En deuxième lieu, ce ne sont pas toutes les solutions qui vérifient (3.2)-(3.5) qui sont des solutions du programme linéaire ; ils doivent en plus satisfaire les contraintes de nonnégativité. Ainsi une procédure algébrique doit être capable d’éliminer, de l’ensemble des solutions qui satisfait (3.2)-(3.1) celles qui n’arrivent pas à satisfaire les contraintes de nonnégativité.

Finalement, une procédure algébrique pour résoudre les programmes linéaires doit être en mesure de choisir parmi les solutions réalisables ceux qui maximisent la fonction objectif.

La méthode de simplexe est une procédure algébrique qui tient compte de ces trois considérations.

Pour illustrer cette procédure, supposons que x2 = 0 et S1 = 0. Notre système devient
    x1 = 150                 x1 =  150
    x1 + S2   = 440        S2 =  340
    4x1 + S3 = 480        S3 =  -120
    x1 + S4     = 90        S4 =  -60

Les variables x1, S2, S3 et S4 (non nulles) sont dites variables de base et les variables S1, x2, (nulles) sont dites variables hors base.

Généralement, si on a un programme linéaire standard constitué de n variables et m contraintes (n ≥ m) alors une solution de base (extrême) est obtenue, en annulant (n-m) variables et en résolvant les m contraintes pour déterminer les valeurs des autres m variables.

On note qu’une solution de base n’est pas toujours réalisable. C’est le cas de la solution qu’on vient de retrouver.

Une solution réalisable de base serait celle où x1 = x2 = 0, ainsi on a :
    S1 = 150
    S2= 440
    S3 = 480
    S4 =   90
Cette solution correspond à un point extrême de l’ensemble des solutions réalisables qui est l’origine O.
Pour la méthode de simplexe une solution réalisable de base initiale est demandée. Une telle solution peut être retrouvée en annulant toutes les variables de décision. Ce qui correspond dans notre exemple au point d’origine O.

A partir de ce point la méthode de simplexe va générer successivement des solutions réalisables de base pour notre système d’équations en s’assurant que la valeur de la fonction objectif est en train d’augmenter jusqu'à localiser la solution optimale du problème qui est un point extrême de l’espace des solutions réalisables donc une solution réalisable de base.

Ainsi, on peut décrire la méthode de simplexe comme étant une procédure itérative qui passe d’une solution réalisable de base à une autre jusqu’à atteindre la solution optimale.

La description mathématique de ce processus fera l’objet de la section suivante.

IV. La méthode des tableaux

La méthode de simplexe commence par l'identification d'une solution réalisable de base et ensuite, elle essaye de trouver d'autres solutions réalisables de base jusqu’à atteindre à la solution optimale. Ainsi, on doit, tout d’abord, retrouver cette solution réalisable de base.


Généralement si le programme linéaire satisfait ces deux propriétés :
P1/ Parmi les variables du problème standard, il y a m variables qui apparaissent avec un coefficient non nul dans chaque contraintes (dans notre exemple : S1, S2, S3 et S4).
P2/  Les valeurs du second membre des contraintes (les composants du vecteur b) sont positives.

Alors une solution réalisable de base est obtenue en  annulant les (n-m) variables de décision et la valeur des variables d'écart est directement donnée par le second membre. La deuxième propriété assure la satisfaction des contraintes de nonnégativité des variables d'écart.
Dans notre exemple, la forme standard du programme linéaire vérifie ces deux propriétés.

a. Tableau de simplexe initial

Après avoir mis le programme linéaire sous une forme qui vérifie les deux propriétés P1 et P2, l’étape suivante est de tracer le tableau de simplexe initial.

Le modèle général des tableaux de simplexe est :













Pour notre exemple le tableau de simplexe initial est le suivant :




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
0
S1
150
1
1
1
0
0
0
0
S2
440
4
2
0
1
0
0
0
S3
480
1
4
0
0
1
0
0
S4
90
1
0
0
0
0
1
On remarque qu’on a placé en première ligne les contributions unitaires de toutes les variables de décision x1,..., S4 dans la fonction objectif. Dans la troisième ligne, on retrouve la première contrainte x1 + x2 + S1 = 150. La valeur 150 représente ici la valeur de S1 relative à la solution réalisable de base initiale. Dans la première colonne on trouve les contributions nulles des variables d'écart qui forment la solution de base initiale.

Exemple :
Question : Quelles sont les contraintes et la fonction objectif du programme linéaire décrit par le tableau de simplexe suivant :




6
7
0
0



x1
x2
S1
S2
0
S1
150
4
2
1
0
0
S2
440
1
5
0
1

Réponse : Les contraintes du programme sont :
        4 x1 + 2x2 + S1  = 50
          x1 + 5x2 + S2  = 40
et la fonction objectif est : 6x1 + 7x2 + 0S1  + 0S2  

Remarque : Les variables qui figurent dans la deuxième colonne sont dites variables de base. A chacune de ces variables, on associe la valeur 1 à l’intersection de la ligne et de la colonne relative à cette variable et dans le reste de la colonne on trouve des zéros.

Jusqu’à ici on a vu comment retrouver une solution réalisable de base et comment présenter le tableau de simplexe initial. Dans la section suivante, on examinera la procédure liée à la méthode de simplexe qui permet de passer de cette solution réalisable de base initiale à une autre solution réalisable de base qui donne une  meilleure valeur de la fonction objectif.

b. Amélioration de la solution

Pour améliorer la solution il faut générer une autre solution de base (point extrême) qui augmente la valeur de la fonction objectif. C’est à dire, qu’on doit sélectionner une variable hors base et une variable de base et les permuter de telle façon que la nouvelle solution donne une plus grande valeur de la fonction objectif.

Pour savoir si on peut améliorer notre solution réalisable de base initiale nous allons introduire deux nouvelles lignes au-dessus du tableau de simplexe.

La première ligne, notée zj, représente la variation de la valeur de la fonction objectif qui résulte du fait qu’une unité de la variable correspondante à la jème colonne de la matrice A est amenée dans la base. Par exemple z1  représente la diminution du profit qui résulte de l’ajout d’une unité à la valeur de x1.
En effet, si on produit un hectare supplémentaire de x1, la valeur de quelques variables de base vont changer vu qu’on a :
     x1 + S1    = 150
    4x1 + S2  = 440
     x1 + S3  = 480
      x1 + S4 =   90
Donc, une augmentation de x1 de 0 vers 1 va être accompagnée d'une diminution des variables de base  S1, S2, S3, S4  respectivement de 1, 4, 1 et 1.
L’effet de cette diminution sur la fonction objectif est nul car les coefficients des variables d’écarts dans cette fonction sont nulles
z1 = 0 × S1 + 0 × S2 + 0 × S3 + 0 × S4 =0 × 1 + 0 × 4 + 0 × 1 + 0 × 1 = 0
La valeur z1 est calculée en multipliant les coefficients de la première colonne de la matrice A relatifs à la variable x1  par les coefficients ci de la première colonne. Généralement, on a :
zj  =
La deuxième ligne, notée cj - zj, représente l’effet net de l’augmentation d’une unité de la jème variable.
Dans notre exemple, l’effet net sur la fonction objectif engendré par l’augmentation d’une unité dans la valeur de x1 est
    c1 - z1 = 100 - 0 = 100

Si on reprend la même opération pour le reste des variables, on trouve le tableau suivant :
   



100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
0
S1
150
1
1
1
0
0
0
0
S2
440
4
2
0
1
0
0
0
S3
480
1
2
0
0
1
0
0
S4
90
1
0
0
0
0
1


zj
0
0
0
0
0
0


cj - zj
100
200
0
0
0
0

En analysant la ligne relative à l’évaluation nette cj - zj, on remarque qu’une augmentation d’une unité de la valeur de x1  engendre un profit de 100 dinars, et qu’une augmentation d’une unité de la valeur de x2 engendre un profit supplémentaire de 200 dinars. Donc, si on a à choisir, on va opter pour une augmentation de la valeur de x2. On dit que x2  est la variable entrante.

Le problème est maintenant, jusqu’où peut-on augmenter x2 ?

Cette augmentation ne peut pas se faire infiniment, sous l’hypothèse que x1  reste nulle. On a
    x1   + S1     = 150
    2x2 + S2    = 440
    4x2 + S3    = 480
    x4 + S2    =   90
On peut voir que x2  peut prendre comme valeur maximale la valeur de 100 (il ne faut pas oublier que les Si, i=1, 2, 3, 4 sont des variables positives). Cette valeur est obtenue en choisissant la plus petite valeur positive des divisions de 100/1, 440/2, 480/4 et 90/0 (on suppose que 90/0 est égale à l’infini ∞).

En général, la valeur maximale de la variable entrante xj est le minimum des valeurs positives des rapports de Qi par les coefficients de la colonne de la matrice A relatif à la jème variable. Ces rapports feront l’objet d’une autre colonne à droite de la matrice A.

Dans notre exemple, on aura :

Le fait d’augmenter x2 jusqu’à la valeur 100 va engendrer l’annulation de la valeur du variable d’écart S3, ce qui élimine S3 de la base. On appelle S3 variable sortante.

L’élément 4, à l’intersection de la ligne relative à la variable sortante S1 (dite ligne pivot) et de la colonne relative à la variable entrante x2 (dite colonne pivot) est l’élément pivot. (C’est l’élément cerclé dans le tableau).

c. Calcul des tableaux suivants

Dans le nouveau tableau de simplexe on va remplacer S3 par x2 et l’ensemble des variables de base deviendra S1, S2, x2, S4. On exige que x2 prenne la même place dans la colonne des variables de base que celle de la variable sortante S3.
Jusqu’à maintenant on ne peut pas remplir le tableau relatif à cette nouvelle solution de base :




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
0
S1







0
S2







200
x2







0
S4








Ce qui reste à déterminer sont les coefficients aij de la nouvelle matrice A et les valeurs Qi des variables de base. Ceci est réalisé en utilisant la règle de pivot :

  1. Diviser le ligne de pivot par la valeur de l’élément de pivot pour trouver la ligne transformée de la ligne de pivot.




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
0
S1







0
S2







200
x2
120
1/4
1
0
0
-1/4
0
0
S4








  1. A chacune des variables de base, on associe la valeur 1 à l’intersection de la ligne et de la colonne relative à cette même variable et dans le reste de la colonne on trouve des zéros.




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
0
S1


0
1
0

0
0
S2


0
0
1

0
200
x2
120
1/4
1
0
0
-1/4
0
0
S4


0
0
0

1

  1. Pour calculer le reste des valeurs du tableau, on opère à des combinaisons linéaires dans le précèdent tableau de simplexe. Par exemple pour calculer la nouvelle valeur qui va prendre la place de la valeur 100 devant la variable de base S1: On multiplie 100 par le pivot (4), on retranche de ce produit le produit de la projection de la valeur 100 sur la ligne pivot par la projection de la valeur 100 sur la colonne pivot, et on divise le tout par la valeur du pivot (4).




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
0
S1
30
3/4
0
1
0
-1/4
0
0
S2
200
7/2
0
0
1
-1/2
0
200
S3
120
1/4
1
0
0
-1/4
0
0
S4
90
1
0
0
0
0
1

Remarques:
  1. On vérifie toujours que les colonnes de la matrice relative à chacune des variables de base sont formées par des zéros sauf 1 dans l’intersection avec la ligne relative aux mêmes variables de base.
  2. On peut vérifier aussi que l’ensemble des solutions réalisables, induit par les contraintes décrites dans le dernier tableau de simplexe, est le même que celui représenté par les contraintes initiales. La règle de pivot est une combinaison linéaire des contraintes du programme linéaire donc elle ne change pas l’ensemble des solutions réalisables.

  1. La nouvelle solution réalisable de base est
    x1 = 0
    x2 = 120
    S1 = 30
    S2 = 200
    S3 = 0
    S4 = 90
Cette nouvelle solution correspond au point A(voir graphique). On vérifie bien que la valeur de la fonction objectif est passer de 0 à 120 x 200. La valeur de la fonction objectif peut être facilement calculer en multipliant membre à membre les ci de la première colonne par les valeurs des variables de base Qi dans la 3ème colonne.
  1. La solution de départ correspond au point O. La première itération nous a amené dans le sens de l'amélioration du profit (fonction objectif), c’est à dire le long de l’axe des ordonnées.

Ayant retrouvé une nouvelle solution, on veut savoir s’il est possible de retrouver une solution réalisable de base meilleure. Pour arriver à cette fin, on doit ajouter les deux lignes relatives au choix de la variable entrante, et la colonne relative au choix de la variable sortante.

La variable entrante est x1 ; elle présente la plus grande valeur cj- zj. Si on calcule les quotients Qi/ci1, on retrouve que la variable sortante est S1  à qui on associe la plus petite valeur du ratio Q1/c11=40. L’élément pivot dans ce tableau est 3/4. La nouvelle base est composée de x1, S2, x2, S4.
Le tableau de simplexe suivant issu de l’application de la règle de pivot est :




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
100
x1
40
1
0
4/3
0
-1/3
0
0
S2
60
0
0
-14/3
1
2/3
0
200
x2
110
0
1
-1/3
0
1/3
0
0
S4
50
0
0
-4/3
0
1/3
1
Cette nouvelle solution
    x1 =   40
    x2 = 120
    S1 =     0
    S2 =   60
    S3 =     0
    S4 =   50
correspond au point B qui est, d’après les résultats retrouvée par la méthode graphique, la solution optimale du problème. Ainsi, il faut s’attendre à ce que la méthode de simplexe reconnaisse cette solution comme étant la solution optimale.

Ajoutons la ligne relative au calcul de l'effet net d’une augmentation unitaire d’une des variables du problème, on a :




100
200
0
0
0
0



x1
x2
S1
S2
S3
S4
100
x1
40
1
0
4/3
0
-1/3
0
0
S2
60
0
0
14/3
1
2/3
0
200
x2
110
0
1
-1/3
0
1/3
0
0
S4
50
0
0
-4/3
0
1/3
1



100
200
200/3
0
100/3
0



0
0
-100/3
0
-100/3
0

L’effet net associé aux variables hors base S1 et S2 est négatif. Ceci nous oblige à dire que faire entrer une de ces deux variables dans la base va engendrer une diminution dans la valeur de la fonction objectif. Donc il n’y a pas une autre solution réalisable de base qui peut engendrer un profit meilleur. Par suite cette dernière solution est la solution optimale. Ce dernier tableau de simplexe est donc dit tableau optimal.

On peut généraliser ce résultat en disant que la solution optimale d’un programme linéaire est atteinte s’il n’y a aucune valeur positive dans la ligne
cj-zj du tableau du simplexe.

V. Résumé de la procédure de la méthode du simplexe

(dans le cas d'un problème de maximisation sous contraintes ≤ et avec un second membre positif)



Etapes
Justification
1. Formuler un programme linéaire pour le problème réel.
Pour obtenir une représentation mathématique du problème
2. Vérifier que le second membre du  programme linéaire est positif
Ceci est nécessaire pour obtenir comme variable de base initiale l’origine
3. Ecrire le programme linéaire sous une forme standard
Mettre toutes les contraintes sous forme d’égalité
4. Construire le premier tableau de simplexe
Ce tableau correspond à la solution initiale de base
5. Choisir comme variable entrante dans la base celle qui admet le plus grand effet net positif cj-zj.
La valeur de cj-zj indique la quantité d’augmentation de la fonction objectif si on augmente la valeur de xj d’une unité.
6. Choisir la variable sortante de la base celle qui admet le plus petit ratio  supérieur à zéro.
La plus petite valeur de Qi/aij indique le nombre maximal d’unité de xj qu’on peut introduire avant que la variable de base de l’ième ligne ne soit égale à zéro.
7. Construire le nouveau tableau en utilisant la règle de pivot
Cette règle nous permet entre autre de calculer les valeurs des nouvelles variables de décision
8. Faire le test d’optimalité. Si
(cj-zj) ≤ 0 pour toutes les variables (hors base), la solution obtenue est donc optimale. Sinon retourner à l’étape 5.
Si (cj-zj) ≤ 0 alors on n’a pas d’intérêt à faire entrer dans la base aucune de ces variables. Une telle introduction engendra une diminution de la fonction objectif.

VI. Exemple

Résoudre le programme linéaire suivant en utilisant la méthode de simplexe.
        Max    3x1 + 2x2
        SC       - x1 + 2x2  ≤ 4
             3x1 + 2x2  ≤ 14
                x1 + x2  ≤ 3
               x1 ≥ 0  x2  ≥ 0
→ La forme standard du programme linéaire s'écrit comme suit :
        Max    3x1  + 2x2
        SC       - x1  + 2x2   +  S1 =  4
             3x1 + 2x2   + S2  =  4
                x1  -  x2     + S3  =  3
               x1, x2, S1, S2, S3≥0


→ Tableau de simplexe initial (1ère itération)


La variable entrante est x1 puisqu’elle présente le plus grand effet net positif. La variable sortante est S3 car elle correspond au plus petit quotient positif.

→ 2ème itération


La variable entrante est x2  et la variable sortante est S2

→ 3ème itération




3
2
0
0
0



x1
x2
S1
S2
S3
0
S1
6
0
0
1
-1/5
8/5
2
x2
1
0
1
0
1/5
-3/5
3
x1
4
1
0
0
1/5
2/5



3
2
0
1
0



0
0
0
-10
0




Tous les cj-zj≤ 0 donc le tableau de simplexe est optimal et la solution optimal du programme linéaire est
    x1 = 4
    x2 = 1
    S1 = 6
    S2 = 0
    S3 = 0
La valeur de la fonction objectif est 14.

Remarque : L’effet net de l’augmentation d’une unité de la valeur de S3 (variable hors base) est nul. Donc si on introduit S3 dans la base, on ne modifie pas la valeur de la fonction objectif. Ainsi une autre solution optimale peut être trouvée pour notre programme linéaire. Ceci confirme le résultat de la méthode graphique qui indique que ce problème admet un ensemble de solution optimale décrit par le segment [BC].

La solution optimale donnée par le dernier tableau de simplexe correspond au point C.
Le tableau du simplexe suivant est :




3
2
0
0
0



x1
x2
S1
S2
S3
0
S3
15/4
0
0
5/8
-1/8
1
2
x2
13/4
0
1
3/8
1/8
0
3
x1
5/2
1
0
-1/4
1/4
0



3
2
0
1
0



0
0
0
-1
0
Le tableau est optimal et la solution correspondante est :
    x1 = 5/2
    x2 = 13/4
    S1 = 0
    S2 = 0
    S3 = 15/4
La valeur de la fonction objectif est 14.

Cours Et Exercices

Commentaires

Enregistrer un commentaire