Résolution d’un programme linéaire (PL) - Cours de La Recherche Opérationnelle
COURS DE LA RECHERCHE OPÉRATIONNELLE
Cours Recherche Opérationnelle
Chapitre 1 : Formulation d’un programme linéaire (PL)I. Introduction
II. Les conditions de formulation d’un PL
III. Les étapes de formulation d’un PL
IV. Présentation Théorique
V. Exemples de formulations
Chapitre 2 : Résolution d’un programme linéaire (PL)
I. Introduction
II. Système d’axes
III. Représentation graphique des contraintes
IV. Représentation de la fonction objectif
V. Recherche de la solution optimale
a. Résolution graphique
b. Résolution par énumération :
VI. Exemples
VII. Analyse de sensibilité
Chapitre 3 :La Méthode de Simplexe
I. Introduction
II. Mise sous forme standard
III. Revue algébrique de la méthode du simplexe
IV. La méthode des tableaux
a. Tableau de simplexe initial
b. Amélioration de la solution
c. Calcul des tableaux suivants
V. Résumé de la procédure de la méthode du simplexe
VI. Exemple
Chapitre 4 : Problèmes de Minimisation et Problèmes Irréguliers
I. Introduction
II. Les variables artificielles
III. Les problèmes de minimisation
IV. Les problèmes irréguliers
a. Les problèmes impossibles
b. Les problèmes à solutions multiples
c. Les problèmes à solution infinie
d. Les problèmes à solution dégénérée
Chapitre 5 : Dualité et analyse de sensibilité
I. Introduction
II. Interprétation économique
III. Dualité
a. Définition
b. Propriétés et signification économique du programme dual
c. Tableau de correspondance primal-dual
III. Analyse de sensibilité
a. Analyse de sensibilité sur les Cj
b. Analyse de sensibilité sur les bj
c. Analyse de sensibilité sur les coefficients aij
IV. Introduction d’une nouvelle activité
a. Introduction d’une nouvelle variable de décision
b. Introduction d’une nouvelle contrainte
Chapitre 6 : Introduction à la Programmation Dynamique
I. Introduction
II. Exemple prototype. Le problème du voyageur
III. Caractéristiques d’un problème de programmation dynamique
IV. Programmation dynamique déterministe
a. Introduction
b. Problème du type plus court chemin
c. Répartition optimale des moyens
d. Résolution d'un programme linéaire
Résolution d’un programme linéaire (PL)
I. Introduction
Après avoir illustrer par des exemples, comment un problème pratique peut être modélisé par un programme linéaire, l’étape qui va suivre sera certainement celle de la résolution de ce problème mathématique. La méthode graphique est l’une des premières méthodes utilisées à ce sujet.
Si on parle de résolution graphique alors on doit se limiter à une représentation à deux variables et au plus à trois variables. Ceci indique que dans ce chapitre on examinera seulement les programmes linéaires à deux variables de décision.
II. Système d'axes
Une des conditions de la réussite de notre représentation graphique est le choix d'un système d’axes. Un mauvais choix peut rendre notre représentation non claire et imprécise.
A cause des contraintes de non-négativité des variables de décision, nous nous intéressons seulement au cadran positif (voir figure ci-dessus).
Cette région s’appelle la région des solutions possibles du problème.
Prenons l’exemple 2 relatif au problème de médecine. Le programme linéaire est le suivant :
Un bon choix se base sur une lecture des différents paramètres du programme linéaire. Dans notre cas, on ne peut qualifier de bon, le choix de 20 comme unité dans les deux axes.
Pour l’exemple, on peut choisir le système d’axes suivant :
III. Représentation graphique des contraintes
Parmi les solutions possibles d’un problème, il y a ceux qui vont satisfaire toutes les contraintes du programme, appelés solutions réalisables, et ceux qui vont satisfaire une partie ou aucune de ces contraintes, appelés solutions non réalisables.
Une représentation graphique des inégalités (des contraintes) va nous permettre de déterminer l’ensemble des solutions réalisables.
Revenons à l’exemple 2 du problème de médecine.
Une des contraintes de ce problème est celle relative au grain d’aspirine :
L’ensemble des solutions qui vérifient cette inégalité est le même que celui qui vérifie  et
et  .
.
L’ensemble des solutions qui correspond à l’équation est l’ensemble des points de la droite l définie par 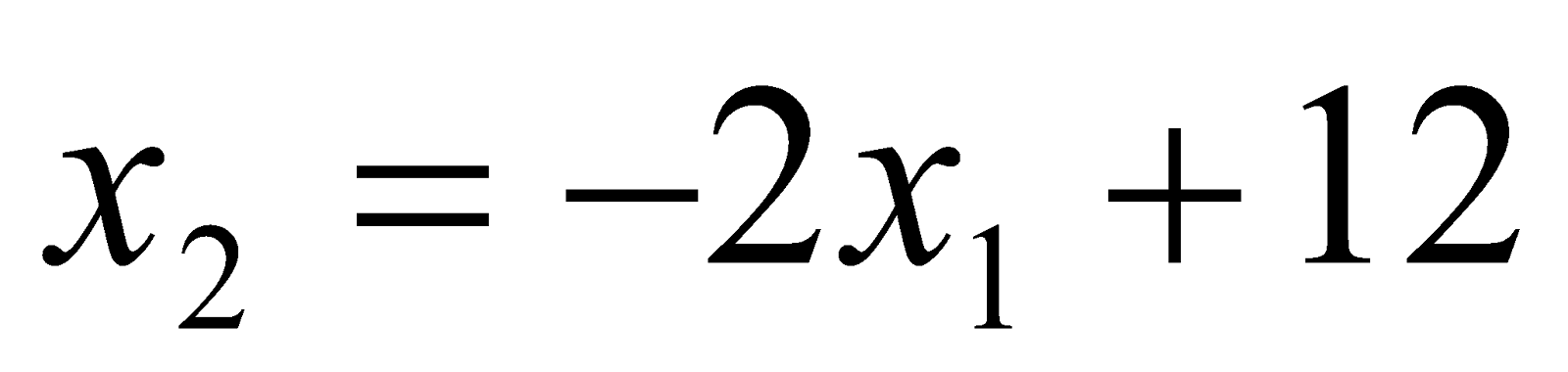 . Cette droite admet une valeur de la pente égale à –2 et intercepte l’axe des ordonnées en 12 (voir figure ci-dessus).
. Cette droite admet une valeur de la pente égale à –2 et intercepte l’axe des ordonnées en 12 (voir figure ci-dessus).
L’inégalité  correspond à un demi-plan limité par la droite
correspond à un demi-plan limité par la droite 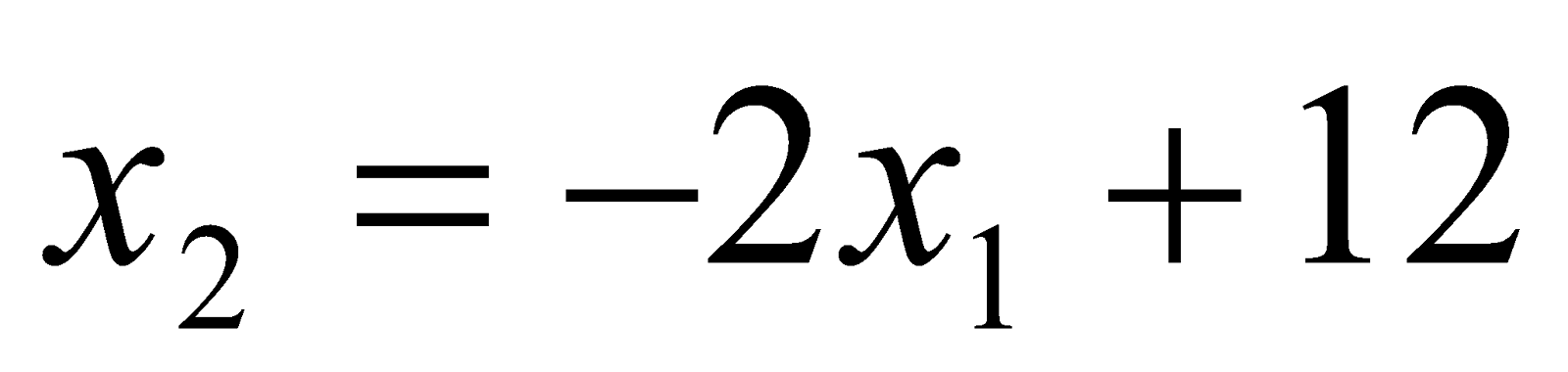 . Or cette droite divise le plan en deux demi-plans ouverts donc quel est le demi-plan à choisir ?
. Or cette droite divise le plan en deux demi-plans ouverts donc quel est le demi-plan à choisir ?
Pour ce faire, il suffit de prendre un point de l’un des demi-plans (c’est à dire n’appartenant pas à la droite 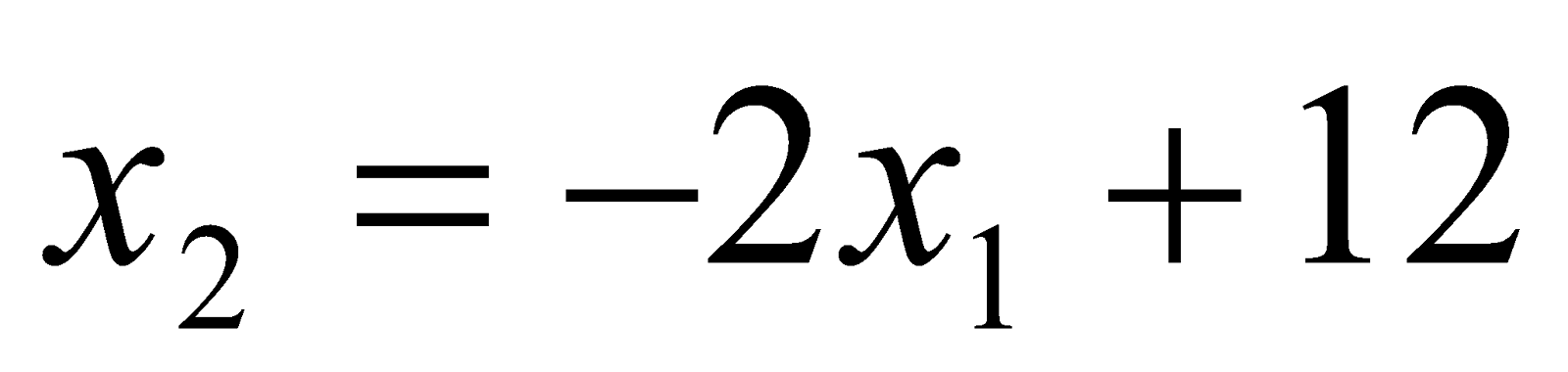 ) et voir s’il vérifie l’inégalité
) et voir s’il vérifie l’inégalité  . Par exemple le point de coordonnées (0,0) ne vérifie pas l’inégalité
. Par exemple le point de coordonnées (0,0) ne vérifie pas l’inégalité  donc le demi-plan π1 au-dessus de la droite est celui recherché (voir figure ci-dessus).
donc le demi-plan π1 au-dessus de la droite est celui recherché (voir figure ci-dessus).
L’espace hachuré représente le demi-plan fermé des solutions qui vérifient la contrainte  .
.
Si on fait de même pour les deux autres contraintes du problème (voir figures
ci-dessous), on obtient les deux autres demi-plans π2 et π3 relatifs aux solutions vérifiant respectivement les contraintes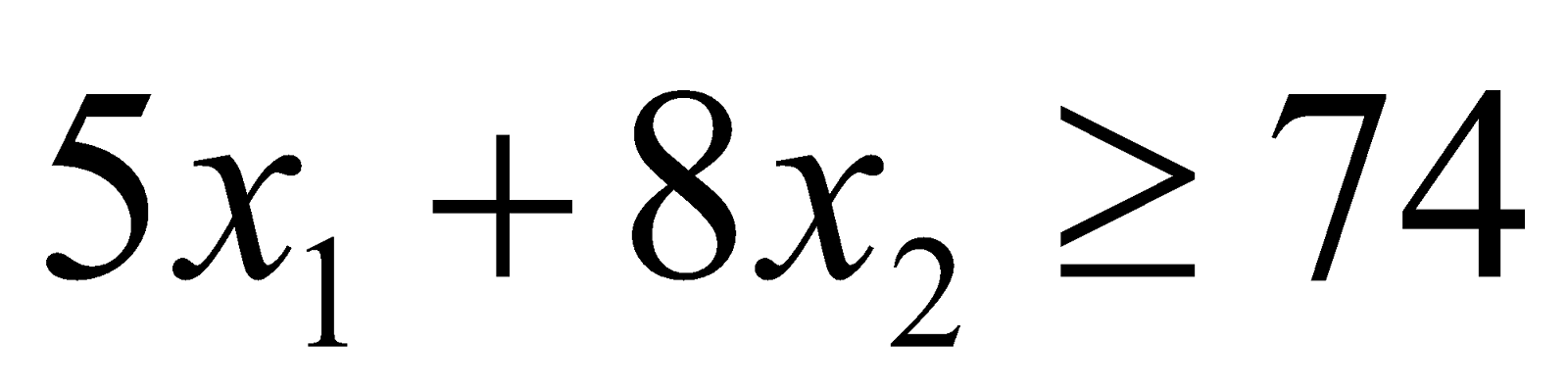 et
et 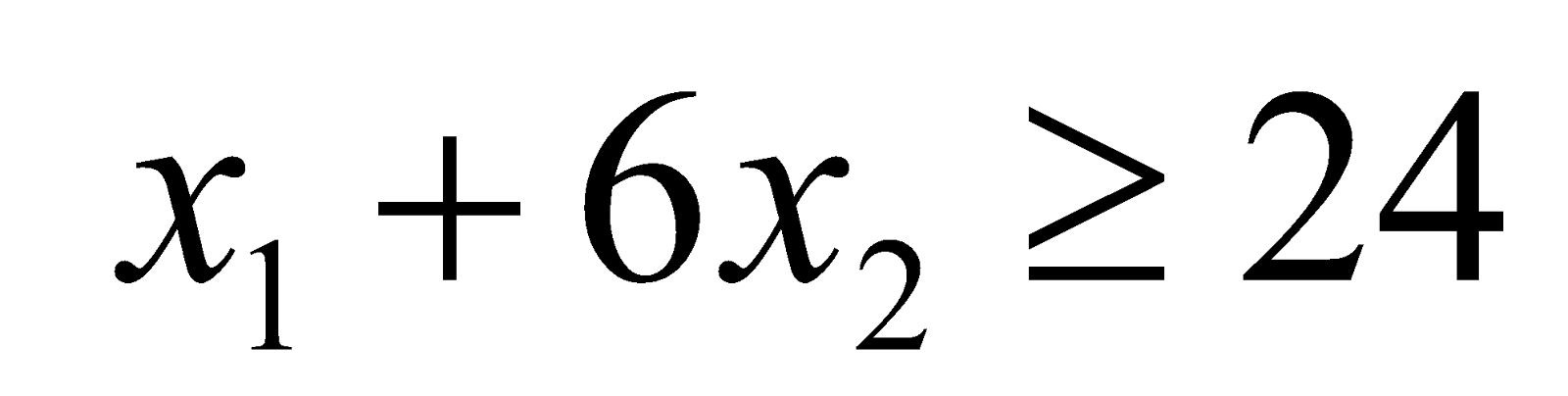 .
.
ci-dessous), on obtient les deux autres demi-plans π2 et π3 relatifs aux solutions vérifiant respectivement les contraintes
Une solution possible du problème est dite réalisable si et seulement si elle vérifie toutes les contraintes, c’est à dire si elle appartient aux trois demi-plans relatifs à chaque contrainte du programme linéaire, en d’autre terme à
π1 ∩ π2 ∩ π3 (voir figure).
π1 ∩ π2 ∩ π3 (voir figure).
Définition : Un ensemble E non vide est dit convexe si et seulement si pour tout élément x et y de E et pour tout λ∈[0,1], λ x + (1-λ) y∈E.
On peut vérifier facilement que chacun des demi-plans π1, π2 , π3 est convexe en vérifiant que pour toute paire de points P1 et P2, l’ensemble des points qui forment le segment [P1P2] appartient au demi-plan.
Théorème : L’intersection d’ensembles convexes (non vide) est convexe.
Propositions : L’ensemble des solutions réalisables (non vide) est convexe.
IV. Représentation de la fonction objectif
Soit z la valeur de la fonction objectif du problème de médecine .
.
Pour z=0, la fonction objectif est représentée de la manière suivante :
Pour z=6, c’est à dire que le nombre de pilules à prescrire est égale à 6 pilules. La fonction objectif est représentée comme suit :
Chaque point du segment qui relie les points (6,0) à (0,6) représente des solutions qui engendrent une prescription avec 6 pilules des deux tailles.
On peut tracer une infinité de droites qui représentent les différentes valeurs de la fonction objectif, toutes ces droites ont le même coefficient directeur (-1). Par suite elles sont parallèles entre elles. De plus on peut diminuer la valeur de z indéfiniment dans le sens indiqué dans la figure ci-dessous.
Le problème est de connaître qu’elle est la droite qui correspond à la valeur minimal de la fonction objectif ?
V. Recherche de la solution optimale
a. Résolution graphique
Si nous retraçons l’ensemble des droites parallèles relatives à différentes valeurs de la fonction objectif sur la figure qui représente l’ensemble des solutions réalisables, on peut localiser la solution optimale. Elle correspond à la solution réalisable qui intercepte la droite à la plus petite valeur de z.
Dans notre exemple, la solution optimale est l’intersection des deux contraintes  et
et 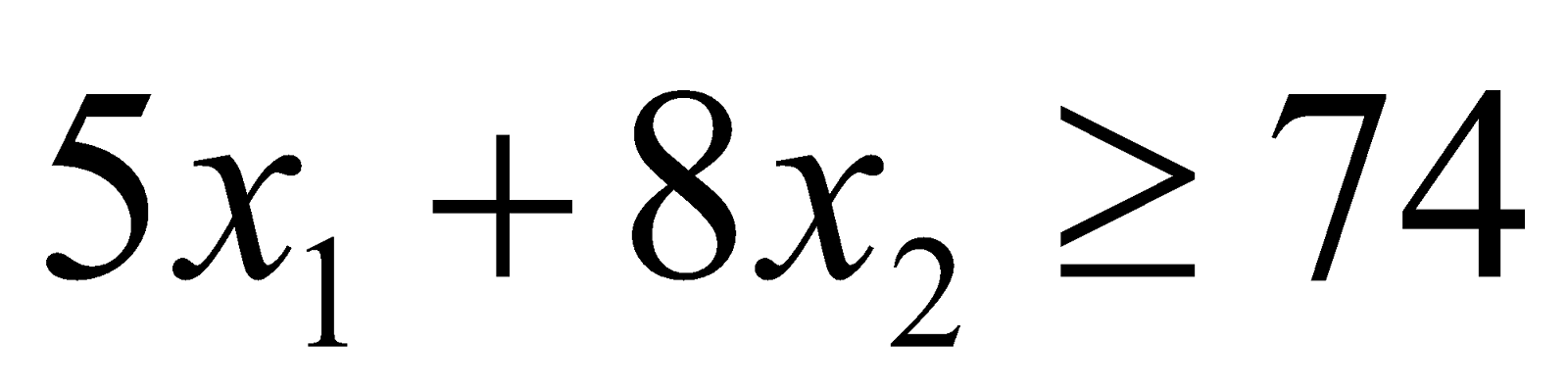 . Une évaluation des coordonnées de ce point revient à résoudre le système linéaire suivant :
. Une évaluation des coordonnées de ce point revient à résoudre le système linéaire suivant :
Elle correspond d’après le graphique au point (2,8). Donc la prescription optimale est de 2 pilules de petite taille et 8 pilules de grande taille. Le nombre de pilules (la valeur de la fonction objectif) est égale à 10.
b. Résolution par énumération
On remarque que la solution optimale du problème de médecine est un point extrême qui se trouve sur le bord de l’ensemble des solutions. Une telle solution est dite solution réalisable de base.
On peut admettre le résultat suivant : « Si un programme linéaire admet une solution optimale alors il existe une solution réalisable de base pour laquelle la fonction objectif atteint la valeur optimale »
Une méthode de résolution du programme linéaire consiste donc à déterminer les solutions réalisables de base (les points d’intersection des droites qui forment les contraintes) et à calculer pour chaque point la valeur de la fonction objectif. La solution du programme linéaire est la solution à qui on associe la valeur optimale de la fonction objectif.
Dans le problème de médecine, l’ensemble des solutions réalisables de base présente 4 points extrêmes A(0,12), B(2,8), C(23/11,126/11) et D(24,0). La valeur de la fonction objectif associée respectivement à A, B, C et D est 12, 10, 149/11 et 24. On vérifie bien que B est la solution optimale du problème avec une valeur optimale égale à 10.
VI. Exemples
Dans cette section on donne quelques exemples de résolution graphique de problèmes linéaires relatifs au différents cas possibles :
Problème de maximisation | |
la solution optimale est B(40,110)
| |
Problème avec solution non bornée | |
On peut augmenter la valeur de la fonction objectif dans la direction des flèches indéfiniment donc la solution est non bornée
| |
Problème impossible | |
L’espace des solutions réalisables est vide, il est l’intersection des deux zones grises de la figure ci-dessus
| |
Problème à solutions multiples | |
L’ensemble des points décrit par le segment [AB] représente les solutions optimales du problème linéaire
| |
Problème de dégénerescence | |
La solution optimale B(10,5) est dite dégénérée si trois contraintes concourent en ce point.
| |
VII. Analyse de sensibilité
Une analyse de sensibilité se résume à la recherche des intervalles de variations possibles des paramètres du programme linéaire sans que la solution optimale ne soit modifiée.
Question : De combien peut-on faire varier la quantité de codéine dans le problème de médecine sans changer la solution optimale.
Réponse :
On peut changer la valeur du second membre de la troisième contrainte jusqu'à ce que la droite de coefficient directeur –1/6 touche le point optimal (2,8). C’est à dire qu’on peut varier le second membre de la troisième contrainte de 24 jusqu'à 50 sans changer la solution optimale.
Question : De combien peut-on faire varier le profit engendré par la culture d’un hectare de tomates, dans le problème de l'agriculture, sans changer la solution optimale ?
Réponse :
Soit λ la variation du profit engendré par la culture d’un hectare de tomate. La fonction objectif est égale à 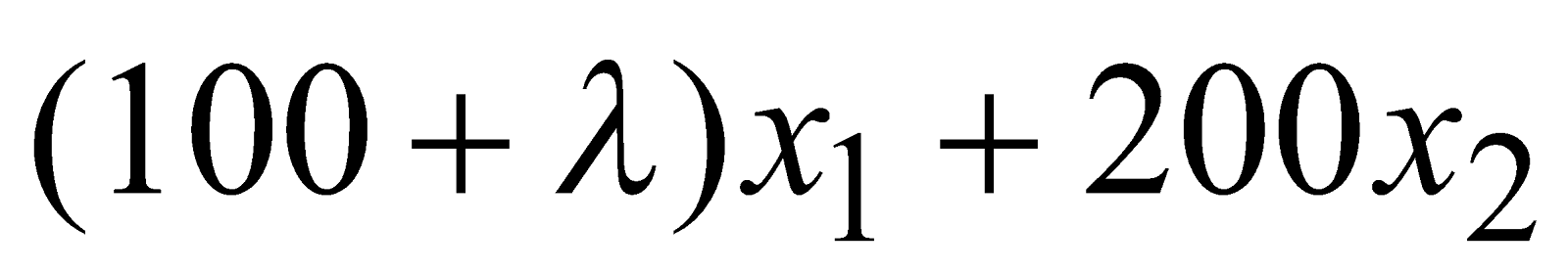
La solution demeure optimale si la pente de la fonction objectif reste toujours comprise entre la pente de la contrainte (1) et (3). Ceci est équivalent à dire que :
On peut vérifier aussi que si :
alors la solution optimale est A
alors le problème est à solutions multiples : [AB]
alors la solution optimale est B
- alors le problème est à solutions multiples : [BC]
alors la solution optimale est C
alors le problème est à solutions multiples : [CD]
alors la solution optimale est D
Commentaires
Enregistrer un commentaire