Disque uniformément chargé avec la densité superficielle uniforme - La solution d'exercice - Exercices corrigés d'életrostatique
a) Calcul du champ électrostatique à partir du potentiel
Le potentiel dV(M) crée en un point M(0,0,z) par la charge dq= σdS entourant le point P (figure 13) est :La charge dq= σdS crée en M le potentiel V(M) s’écrit :
Ce qui donne :
Le potentiel V(M) est obtenu par intégration sur la surface du disque :
 est déduit du potentiel par dérivation :
est déduit du potentiel par dérivation :b) Calcul direct du champ en un point M(0,0,z)
Examinons d’abord la symétrie du problème : la distribution présente une symétrie de révolution autour de . Tout plan contenant l’axe
. Tout plan contenant l’axe  est un plan de symétrie paire de la distribution. Donc le champ
est un plan de symétrie paire de la distribution. Donc le champ  en un point M de l’axe
en un point M de l’axe  est porté par
est porté par  :
:Un élément de charge dq= σdS , centré en P (figure 13), crée en un point M de l’axe du disque un champ élémentaire
 donné par :
donné par : Le disque chargé présente une symétrie de révolution autour de son axe, par exemple l’axe z’z, le champ est alors porté par cet axe. On a :
avec, ρ variable radiale cylindrique
Loin du disque (z grand), le champ s’affaiblit (figure 14).
Cas limites
• Si le point M est très éloigné du disque, c’est à dire : |z| >> R, on aura alors :
C’est l’expression du champ créé en M par une charge Q =σΠR² placée en O.
• Si le point M est très proche du disque, c’est à dire |z| << R, on aura :
C’est l’expression du champ créé en M par un plan (infini) uniformément chargé
Conséquence
A la traversée du disque, le champ normal au disque subit une discontinuité égale à :
Ce résultat est valable pour n’importe quelle distribution de charges en surface, uniforme ou non : si σ est la densité locale d’une distribution surfacique quelconque de charges, il y a en ce point un changement brutal (discontinuité égale à σ/ε0) de la composante du champ électrostatique perpendiculaire à la surface.











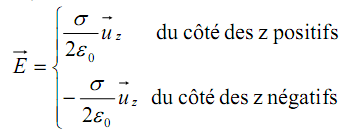

Commentaires
Enregistrer un commentaire