Boucle circulaire portant une charge linéique uniforme - La solution d'exercice - Exercices corrigés d'életrostatique
a) Calcul du champ électrostatique à partir du potentiel
Le potentiel dV(M) créé en un point M(0, 0, z) par la charge dq=λdl portée par un élément dl de la boucle entourant P (figure 8) est :
La charge dq=λ0dl=λ0Rdθ crée en M le potentiel V(M) :
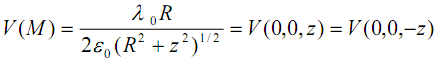
Le champ
est déduit du potentiel par dérivation : 
b) Calcul direct du champ en un point M(0,0,z)
Examinons d’abord la symétrie du problème : la distribution présente une symétrie de révolution autour de
. Tout plan contenant l’axe est un plan de symétrie paire de la distribution. Donc le champ E en un point de l’axe est porté par 
: 
étant porté par, seule la composante dEz est à considérer :