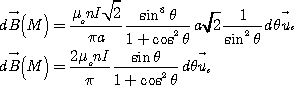La solution d'Exercice sur Solénoïde de section carrée (Champ magnétique)
1. Expression du champ.
On considère une « collection »
de spires comprises entre les cotes z et z
+ dz autour d’un point P créant en
M un champ magnétique élémentaire
d’expression :
avec
On obtient une nouvelle expression du champ élémentaire :
Le champ magnétique s’écrit
alors :
On effectue un changement de
variable en posant : 
et
et
On obtient ainsi :
2. Cas où l >> a.
Dans le cas où l >> a
on peut poser que
et que
Avec ces approximations on obtient :
et que Avec ces approximations on obtient :
3. Champ loin des faces.
Dans ces conditions on peut
effectuer les approximations suivantes :
et
et
On obtient alors :
La démonstration relative au
solénoïde infini fait intervenir des considérations
de symétrie, d’invariance par translation suivant
l’axe Oz ¸le théorème d’Ampère et en rien la
forme des spires constituant le solénoïde. C’est
pour cela que l’on retrouve le résultat classique du
solénoïde à spires circulaires.
4. Cas du solénoïde infini.
Tout plan perpendiculaire à
l’axe du solénoïde est plan de symétrie de la
distribution de courants. Cette constatation permet
d’affirmer alors qu’en tout point intérieur ou
extérieur au solénoïde le champ magnétique a une
direction parallèle à celle de l’axe de ce
solénoïde.
Les lignes de champ magnétique
sont alors des droites parallèles à l’axe Oz.
D’autre part il y a invariance
de la situation physique lors d’une translation le
long de l’axe Oz, le champ magnétique garde
alors une valeur constante le long d’une ligne
champ.
On applique le théorème
d’Ampère :
Pour une courbe fermée à
l’intérieur ou à l’extérieur du solénoïde, il n’y a
pas de courants enlacés. On alors :
Comme
on a
on a 
Le champ magnétique est
uniforme à l’intérieur comme à l’extérieur du
solénoïde mais pas avec la même valeur. En effet,
les spires sont assimilables à une distribution
surfacique de courants et il y alors discontinuité
de la composante tangentielle du champ magnétique à
la traversée des spires.
(et cela d’après la question 3 et des résultats
précédents). Pour déterminer le champ à l’extérieur
on considère un nouveau contour d’Ampère comme
indiqué sur la figure suivante :
Le théorème d’Ampère permet
d’écrire que :
On retrouve bien ainsi la
discontinuité de la composante tangentielle du champ
magnétique à la traversée d’une nappe de courants.