Exercice corrigé sur Action d'un champ magnétique. Déflexion magnétique. Mouvement hélicoïdal.(Mouvements d'une particule chargée dans un champ électromagnétique)



Voir la solution

Des électrons non relativistes de masse m, de charge -e pénètrent dans une région Ω d'épaisseur L où règne un champ magnétique uniforme perpendiculaire à la vitesse incidente des électrons.

  1. Les électrons arrivent à t = 0 au point O avec une vitesse initiale  colinéaire à l'axe Oz. Le champ  sera dirigé selon Oy. La région Ω est comprise entre les plans z = 0 et z = L. Montrer que la trajectoire décrite par un électron dans la région Ω est circulaire. Préciser en particulier le rayon de cette trajectoire  et la pulsation  du mouvement en fonction de m, e,  et B.
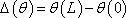
  2. Quelle déviation  a subi la trajectoire d'un électron à la sortie de la régionΩ,  étant l'angle que fait la vitesse de l'électron à l'abscisse z avec l'axe Oz.
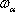
  3. La vitesse incidente des électrons à l'entrée de la région Ω fait maintenant un angle α avec la direction du champ B (tout en étant perpendiculaire à Ox). Montrer que le mouvement de l'électron est alors hélicoïdal, c'est-à-dire qu'il résulte de la composition d'un mouvement circulaire uniforme  (dont on précisera la pulsation  et le rayon  en fonction de ,  et de l'angle α), et d'un mouvement rectiligne uniforme dont on précisera la vitesse .
  4. Déterminer le pas de l'hélice, c'est-à-dire la distance parcourue selon l'axe pendant une période de rotation.

Voir la solution


 

Cours Et Exercices