Arrangement sans répétition :DÉNOMBREMENT
Définition 1
Soit E ={x1,x2,…,xn}, un ensemble fini à n éléments Choisissons successivement p éléments deux à deux distincts, et disposons les en p-uplet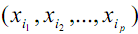
une telle liste ordonnée est appelée p-liste sans répétition d’éléments de E .
On dit encore arrangement sans répétition d’ordre p d’élément de E
Proposition 1:
Supposons le Card(E) = n. Il y a n(n-1)…(n-p+1) listes sans répétition de E.
Preuve :
Le premier élément xi1 peut être choisi de n façons, le deuxième xi2 de ( n-1) façon,…, le pième xip de (n- p+1) façons. Au total, il y a donc n.(n-1)(n-p+1)
façons de constituer le p-uplet (xi1, xi2, …,xip)
Cet entier sera noter :
Les arrangements sans répétition d’ordre p peuvent être décrits d’une autre manière Le p uplet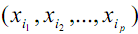 définit l’injection suivante :
Définition 2 :
On appelle donc également arrangement d’ordre p de E, toute injection de {1,2,...,p}dans E.
Permutation d’un ensemble fini.
Le nombre de bijections de E dans E.
Proposition 2 :
Il y a n ! bijections d’un ensemble de cardinal n dans lui-même.
On appelle permutation de E, toute bijection de E dans E.
Soit E ={x1,x2,…,xn}, un ensemble fini à n éléments Choisissons successivement p éléments deux à deux distincts, et disposons les en p-uplet
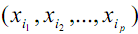une telle liste ordonnée est appelée p-liste sans répétition d’éléments de E . On dit encore arrangement sans répétition d’ordre p d’élément de E
Proposition 1:
Supposons le Card(E) = n. Il y a n(n-1)…(n-p+1) listes sans répétition de E.
Preuve :
Le premier élément xi1 peut être choisi de n façons, le deuxième xi2 de ( n-1) façon,…, le pième xip de (n- p+1) façons. Au total, il y a donc n.(n-1)(n-p+1)
façons de constituer le p-uplet (xi1, xi2, …,xip)
Cet entier sera noter :
Les arrangements sans répétition d’ordre p peuvent être décrits d’une autre manière Le p uplet
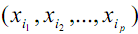définit l’injection suivante : 
Définition 2 :
On appelle donc également arrangement d’ordre p de E, toute injection de {1,2,...,p}dans E.
Permutation d’un ensemble fini.
Le nombre de bijections de E dans E.
Proposition 2 :
Il y a n ! bijections d’un ensemble de cardinal n dans lui-même.
On appelle permutation de E, toute bijection de E dans E.