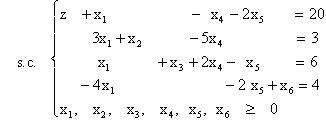Exercices corrigés recherche opérationnelle
Méthode du Simplexe Voir solutions des exercices
S1) Ecrivez le problème PL suivant sous forme standard avec des
M.d.D. non négatifs:s:
Max z = 2x1 + 3 x2 + 5 x3
Formulez son dual.
S2) Considérons l’ensemble de contraintes suivant:
Résolvez
par la méthode du simplexe le problème obtenu lorsque la fonction objectif est
donnée par:
a)
|
max z
|
=
|
2x1
|
+ x2
|
- 3x3
|
+ 5x4
|
b)
|
max z
|
=
|
- 2x1
|
+ 6x2
|
+ 3x3
|
- 2x4
|
c)
|
max z
|
=
|
3x1
|
- x2
|
+ 3x3
|
+ 4x4
|
d)
|
min z
|
=
|
5x1
|
- 4x2
|
+ 6x3
|
+ 8x4
|
e)
|
min z
|
=
|
3x1
|
+ 6x2
|
- 2x3
|
+4x4
|
S3) Résolvez le problème suivant par la méthode du simplexe
max z = 5x1 + 4x2
+ 3x3
S4) Résolvez le problème suivant par simple inspection, puis par la
méthode du simplexe
max z = 5 x1 - 6 x2
+ 3 x3 - 5 x4 + 12 x5
S5) Résolvez le problème suivant
par la méthode du simplexe :
On
doit organiser un pont aérien pour transporter 1600 personnes et 90 tonnes de
bagages. Les avions disponibles sont de deux types: 12 du type A et 9 du type
B. Le type A peut transporter, à pleine charge, 200 personnes et 6 tonnes de
bagages. Le type B, 100 personnes et 6 tonnes de bagages. La location d’un
avion du type A coûte 800.000 F; la location d’un avion du type B coûte 200.000
F.
S6) Les
dictionnaires ci-dessous ont été obtenus après exécution de quelques itérations
de la méthode du simplexe sur différents problèmes. Quelles conclusions
pouvez-vous tirer sur base de l’information contenue dans ces dictionnaires?
Les
conclusions possibles sont par exemple:
.
la solution courante est optimale, et vaut ...;
.
le problème est non borné parce que ...;
.
le problème est non réalisable parce que ...;
.
la solution courante n’est pas optimale; dans ce cas, calculez la solution
optimale.
a) min z
b) max z
c) max z
Dualité & Sensibilité
DS1) Suite de l’exercice S6a).
Quel
est le coût réduit de chacune des variables du problème?
DS2) Suite de l’exercice S3).
a) Si le coefficient de la variable x2
dans la fonction objectif augmentait de 2 unités, quel serait l’effet produit
sur la solution optimale et la valeur optimale du problème? Et si cette
augmentation était de 4 unités?
b)
Quel est le coût réduit de chacune des variables du problème?
c)
Quel est le prix dual de chacune des contraintes d’inégalité du problème?
DS3) Considérons le programme linéaire suivant, exprimé sous forme
standard:
min z
= 2x1 +
x2
a) Calculer le dictionnaire associé à la base B définie
par les variables de base x1, x2, x5 .
b) La solution de base associée à B est-elle réalisable
et optimale?
DS4) Soit le problème (P):
max z = 2x1
+ 4x2 + 4x3 - 3x4
La base optimale de (P) est
et son inverse
a) Formulez
le problème dual de (P).
b) Sur base des informations fournies (et
donc, sans utiliser la méthode du simplexe ni la méthode
graphique), calculez la solution optimale de (P) et celle de son dual.
Expliquez la méthode que vous utilisez.
c) Si la
fonction objectif de (P) est remplacée par
max z = 3x1
+ 4x2 + 4x3 - 3x4 ,
la base B donnée ci-dessus reste-t-elle optimale? Justifiez votre
réponse.
DS5) Soit le problème suivant (P):
max z = 100x1
+ 50x2 + 25 x3
La base optimale de (P) est
a) Ecrivez le dual de (P)
b) Quelle est la solution
optimale du programme (P) et celle de son dual?
DS6) Soit le problème de programmation linéaire
max z = 60x1
+ 30x2 + 20x3
La
résolution de ce problème par la méthode du simplexe permet de calculer la base
optimale
a) Calculez la solution
optimale et la valeur optimale du problème.
b) Calculez et interprétez le
prix dual de la contrainte (2).
DS7) Soit le problème de programmation linéaire
max z = 30 x1 + 20x2
a) Résolvez le problème
graphiquement.
b) Sur base de a), déterminez
la base optimale B.
c) Pourrait-on déduire les prix
duaux sur base de cette information?
DS8) Soit le problème de programmation linéaire (P):
min z = 500x1 + 500x2 +
500x3 + 300x4 + 425x5
A l’optimum de (P), on a x1 = x2 = x3 = x5 =
0
a) Trouvez la solution optimale
et la matrice de base optimale pour (P).
b) A partir de la matrice de
base, calculez la valeur optimale des variables duales.
c) Ecrivez le problème dual de
(P).
DS9) Soit le problème de programmation linéaire
max z = 4x1 + 5x2 + 6x3
a) Formulez le dual et
résolvez-le (par inspection)
b) Utilisez a) et le théorème
de dualité forte pour résoudre le primal.
DS10) Soit le problème de programmation linéaire:
min z =
2x1 + 3x2
Son dual
s’écrit
max w
= 30y1 +
10y2
Déterminez si les solutions suivantes sont réalisables et optimales:
a) ( x1 = 10, x2
= 10/3; y1 = 0, y2 = 1, y3 = 1)
b) (x1 = 20, x2
= 10; y1 = 1, y2
= 4, y3 = 0)
c) (x1 = 10/3,
x2 = 10/3; y1 = 0, y2 = 5/3, y3 =
1/3)
DS11) Considérons le programme
linéaire suivant
max z
= 5x1 + 2x2 + 3x3
La solution optimale est donnée
par le dictionnaire final
max z
a) Ecrivez le problème dual
associé.
b)
Déterminez la matrice de
base optimale B. Déduisez-en la solution optimale du dual.
c) Dans quel intervalle peut
varier c1 (idem c2, c3) sans affecter
l’optimalité de la solution?
d) Dans quel intervalle peut
varier b1 (idem b2) sans affecter l’optimalité de la base
B?
e) Déterminez les prix duaux.
DS12) Considérons le problème de
l’exercice DS11.
a) Supposons que le M. de D.
des contraintes devienne (30 + q, 40 - q), où q est un paramètre non
négatif. Déterminez les valeurs de q pour lesquelles
la base B reste optimale.
b) Pour
chacune des fonctions objectif suivantes, trouvez la nouvelle solution optimale
en utilisant la procédure d’analyse de sensibilité.
i) max z = 12x1 + 5x2
+ 2x3
ii) min z =
2x2 - 5x3
DS13) Voici la formulation d’un
petit problème de transport impliquant 3 entrepôts et 2 clients:
min z =
3x11 + 2x12 + 4x21 + x22 + 2x31
+ 3x32
(remarquez que le problème est non équilibré).
Ce
problème a été mis sous forme standard en introduisant des variables d’écart s1 , s2 et s3 dans
les trois premières contraintes, puis résolu par un logiciel utilisant la
méthode du simplexe. Voici quelques informations sur la solution optimale:
·
les variables en base à
l’optimum sont x11, x12, x22, x31
et s1;
·
le coût réduit de x21
et celui de x32 sont égaux à
2;
·
les prix duaux des
contraintes sont donnés par (y1, y2, y3, y4,
y5) = (0, -1, -1, 3, 2).
a) Mettez le problème sous
forme standard (comme suggéré ci-dessus) et formulez son problème dual.
b) Utilisez l’information
donnée plus haut pour calculer la solution optimale du problème et le coût de
transport correspondant.
c) Si le coût unitaire de
transport entre l’entrepôt 2 et le client 1 diminuait de 1 unité (passant ainsi
de 4 à 3), quelle serait l’incidence de ce changement sur la solution optimale
et la valeur optimale calculées précédemment?
d) Le gestionnaire du troisième
entrepôt s’aperçoit qu’il a commis une erreur en évaluant ses stocks: il
possède en fait 55 unités en stock. En supposant que la base optimale ne soit
pas affectée, quel sera l’effet de cette correction sur le coût de transport
optimal?
Files d’attente
F1) Le
responsable d’un parking du centre-ville a compté le nombre de voitures garées
dans son parking à différents instants de la journée. En moyenne, il en a
trouvé 150. Il sait par ailleurs que, toujours en moyenne, 40 voitures par
heure pénètrent dans le parking et y trouvent une place.
Estimez
le temps moyen passé par chaque voiture dans le parking. Expliquez votre
approche.
F2) Des
clients arrivent dans un restaurant selon un processus de Poisson au taux de 20
clients par heure. Le restaurant ouvre ses portes à 11 heures.
Trouvez:
a) la probabilité d’avoir
20 clients dans le restaurant à 11 h 12 sachant qu’il y en avait 18 à 11 h 07.
b) la probabilité qu’un
nouveau client arrive entre 11 h 28 et 11 h 30 sachant que le dernier client
est arrivé à 11 h 25.
F3) Des
patients arrivent à une clinique selon un processus de Poisson. On dispose de
l’information suivante: si X représente l’intervalle de temps écoulé entre deux
arrivées successives, alors
Pr [x > 30½x > 15] = 0,6
Soit
N(t) le nombre de clients qui se présentent durant un intervalle de t minutes.
Calculez
Pr [ N(15) = 0 ]. Justifiez votre réponse.
F4) Les
articles d’un stock sont vendus selon un processus de Poisson au taux de 5
articles par jour. Le stock initial est de 80 articles.
a) Trouvez la probabilité que 10 articles
soient vendus durant les 2 premiers jours.
b) Déterminez la probabilité qu’il n’y ait
plus d’articles en stock après 4 jours.
c) Déterminez le nombre moyen d’articles
vendus sur une période de 4 jours.
F5) Des
clients se présentent à une agence de banque au rythme moyen de 10 clients par
heure. Ils y sont servis par l’unique employé de l’agence, auprès duquel chaque
client passe 5 minutes en moyenne. Selon les données recueillies par le
directeur de l’agence, les arrivées de clients et les temps de service semblent
caractéristiques de processus de Poisson.
a) Quel modèle décrit adéquatement ce
système? Expliquez.
b) Estimez le temps moyen passé par chaque
client dans le système.
Le directeur de
l’agence décide de licencier son employé et de le remplacer par un employé plus
qualité, x fois plus rapide que l’employé actuel, où x est un paramètre au
moins égal à 1.
c) Estimez
le temps moyen passé par chaque client dans ce nouveau système.
d) Que
doit valoir x pour que le temps ainsi calculé en c) soit réduit à 5 minutes?
F6) Un aéroport possède une seule piste
réservée aux décollages (et une autre réservée aux atterissages). En moyenne,
la tour de contrôle reçoit 15 demandes d’autorisation de décoller par heure;
ces demandes surviennent selon un processus de Poisson. Par ailleurs, la durée
moyenne de chaque décollage est de 3 minutes, mais varie de façon aléatoire
selon une loi exponentielle (par « durée de décollage », on entend le
temps écoulé entre le moment où la tour donne à un avion l’autorisation de
décoller et le moment où elle peut accorder cette autorisation à un (éventuel)
avion suivant).
a) Quel
modèle décrit adéquatement ce système? Expliquez.
b) Estimez le nombre moyen d’avions en
file d’attente, c’est-à-dire ayant demandé, mais pas encore reçu,
l’autorisation de décoller.
c) Estimez le temps moyen passé par chaque
avion en file d’attente (défini comme en b)).
d) Quelle est la probabilité qu’un avion
qui demande l’autorisation de décoller ne reçoive pas immédiatement cette
autorisation, et doive donc attendre?
e) Par mesure de sécurité, on voudrait
réduire à 2 le nombre moyen d’avions gérés par la tour de contrôle
(c’est-à-dire, en file d’attente ou en cours de décollage) à tout instant. A
combien faut-il réduire la durée moyenne de chaque décollage pour atteindre ce
but?
F7) Des
voitures arrivent à un poste de péage selon un processus de Poisson avec une
moyenne de 90 voitures par heure. Le temps moyen de passage à ce poste est de
38 secondes. Les automobilistes se plaignent de longues attentes à ce poste.
Les autorités locales désirent alors réduire le temps de passage à 30 secondes
en installant un nouveau dispositif automatique. Mais cette modification sera
justifiée seulement si, sous l’ancien système, le nombre moyen de voitures dans
la file dépasse 5. De plus, le pourcentage de temps creux (c’est-à-dire sans
voitures) sous le nouveau système ne devrait pas excéder 10%.
Le
nouveau dispositif peut-il être jusitifié?
F8) L’infirmerie
d’une grosse entreprise emploie deux infirmières qui s’occupent des incidents
bénins (petits accidents, malaises, etc.) survenant durant les heures de
travail. Les arrivées des patients à l’infirmerie forment approximativement un
processus de Poisson; en moyenne, il arrive deux patients par heure. Chaque
patient est soigné par une seule infirmière (elles ont des qualifications
identiques) et le traitement dure une demi-heure en moyenne (la durée du
traitement suit une loi exponentielle).
a) Quel modèle de files
d’attente décrit-il adéquatement cette situation? Précisez tous les paramètres
du modèle.
b) En moyenne, combien de
patients se trouvent-ils dans la file d’attente à un instant quelconque de la
journée? Combien de temps doivent-ils attendre avant d’être pris en charge par
une des infirmières?
F9) Une agence de banque est
modélisée par un système de files d’attente M/M/2. Les clients s’y présentent
au rythme de 8 clients par heure. Le temps de service est de 5 minutes par
client.
a) Quelle est la
distribution de probabilité de la variable aléatoire « temps écoulé entre
deux arrivées de clients successives »?
b) Calculez la probabilité
qu’un client qui se présente à l’agence soit servi sans attendre.
c) Calculez le temps d’attente moyen par
client.
d) Interprétez ce système
M/M/2 comme un processus de naissance et de mort particulier.
(Quelle
est la valeur des paramètres de ce processus?)
F10) Dans un système de files
d’attente M/M/2 le temps de service moyen est de 5 minutes et la durée moyenne
entre deux arrivées successives est de 8 minutes.
a) Quelle est la
probabilité qu’un client qui se présente doive attendre?
b) Quelle est la
probabilité qu’un serveur au moins soit libre?
c) Quelle est la
probabilité que les deux serveurs soient libres?
F11) Etablissez le diagramme de
transition et les équations d’équilibre d’un système de files d’attente M/M/3
dans lequel un maximum de 5 clients peuvent être simultanément présents.
Déterminez les
probabilités à long terme pn (n ³ 0).
F12) Un système de files
d’attente ne peut contenir plus de 4 clients.
Le taux d’arrivée est l = 10 clients par heure et
le taux de départ est m = 5 clients par
heure. Ces deux taux sont indépendants du nombre n de personnes dans le système.
Nous supposons que les processus d’arrivée et de départ suivent une
distribution de Poisson. Dessinez le graphe de transition; puis déterminez ce
qui suit:
a) les équations
d’équilibre décrivant le système;
b) les probabilités
stationnaires;
c) le nombre moyen Ls
de clients dans le système;
d) le taux d’arrivée moyen
leff;
e)
le temps moyen Wq
passé dans la file.