épartition volumique de charges comprise entre deux calottes sphériques - La solution d'exercice - Exercices corrigés d'életrostatique

1) Charge totale comprise entre deux calottes sphériques chargées en volume 

La charge totale Q de la répartition est donnée par : 

dτ est exprimée en coordonnées sphériques 

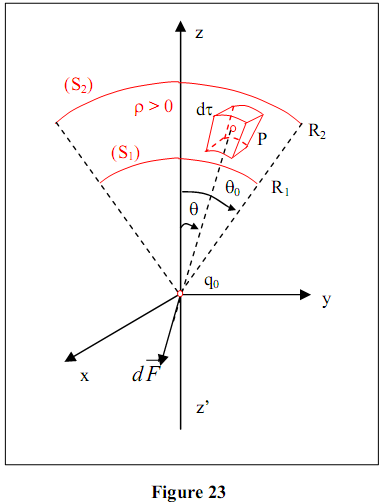Là encore, d’après la symétrie de révolution autour de z’z, présentée par la charge répartie dans le volume considéré (figure 23), la force exercée sur q₀, placée en O, est portée par z’z : 

2) Force exercée par une répartition volumique de charge  comprise entre deux calottes sphériques sur une charge ponctuelle 

Remarquons de même que dans le cas d’une couche sphérique ( θ₀=Π ), le même type de raisonnement de symétrie que celui appliqué dans l’exemple précédent conduit à une force résultante nulle en O . 

∎ Retour Aux Exercices