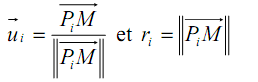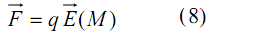Charge Et Interaction Electrostatiques - Cours d’électrostatique
CHARGE ET INTERACTIONS ELECTROSTATIQUES
1- INTRODUCTION
L'électrostatique est la branche de la physique qui étudie les phénomènes (champ et potentiel électrostatique) créés par des charges électriques statiques pour l'observateur. Les forces électrostatiques sont décrites par la loi de Coulomb qui présente une certaine analogie avec l’interaction gravitationnelle.2 - LA CHARGE ELECTRIQUE
2.1 - Définition
La charge électrique d’une particule est une grandeur scalaire (algébrique) qui caractérise les actions électromagnétiques subies ou exercée par la particule.La charge électrique joue dans l’interaction électrostatique le même rôle que joue la masse (scalaire positive) dans l’interaction gravitationnelle.
Les expériences d’électrisation montrent qu’il existe deux classes de particules chargées : deux particules chargées d’une même classe se repoussent alors que deux particules chargées appartenant à des classes différentes s’attirent. Par convention, l’une des classes sera dite chargée positivement, l’autre chargée négativement. Ainsi, si le proton est affecté d’une charge positive et l’électron d’une charge négative, aucune considération physique ne peut justifier ce choix qui n’a aucune incidence sur la théorie de l’électromagnétisme.
2.2 - Quantification de la charge
A l’échelle microscopique, l‘expérience montre (Millikan, 1913), montre que la charge électrique varie de façon discontinue et se présente par unité sous forme de quantité bien déterminée. On dit qu’elle est quantifiée. Sa valeur est un multiple entier d’une charge qu’on peut prendre comme charge élémentaire, notée e. C’est la valeur absolue de la charge de l’électron e = 1,60219 10-19C.
Les particules élémentaires, constituants de la matière, ont pour charges:
- électron : q = -e = - l,60 10-19 C
- proton : q = + e = l,60 10-19 C
- neutron : la charge est nulle.
L’unité de la charge est le coulomb C dans le SI. (MKSA). C’est la quantité de charge transportée par un courant de 1 Ampère pendant 1 seconde (Q = I t).
1 C = 6,25 1018e
C’est un nombre élevé de particules. Dans la pratique, on utilise le mC et le μC.
Notons, qu’à l’échelle macroscopiques (grand nombre de charge élémentaires) la nature discontinue de la charge n’a plus de sens : la charge électrique paraît être une grandeur susceptible de variation continue.
2.3 - Invariance de la charge électrique
Le principe de conservation de la charge est des principes fondamentaux de conservation qui sont à la base de la physique, tels que la conservation de l’énergie, de la quantité de mouvement, du moment cinétique, ...La charge totale d’un système n’est pas modifiée par suite du mouvement des charges.
La loi de conservation de la charge est valable en relativité, c’est-à-dire même si la charge se déplace à une vitesse proche de celle de la lumière. On dit que la charge électrique est une grandeur qui est conservée : c’est un invariant relativiste. Des expériences ont permis de montrer que la valeur de la charge d’un électron ne dépend pas de sa vitesse : la valeur est donc la même pour un observateur en mouvement par rapport à la charge. Ce n’est pas le cas de toutes les grandeurs physiques : l’énergie est conservée mais n’est pas un invariant relativiste.
3 - LOI DE COULOMB OU PRINCIPE FONDAMENTAL DE L’ELECTROSTATIQUE
Nous commencerons par analyser l’interaction électrostatique (forces et champ) dans le cas de charges ponctuelles. Par charges ponctuelles nous voulons signifier que les dimensions des chargées sont petites par rapport à la distance qui les sépare ; ce n’est donc qu’une idéalisation mathématique d’un système physique. La généralisation de ces notions au cas d’une distribution continue de charges sera faite dans le chapitre II.3.1 - Enoncé de la loi de Coulomb
Considérons dans le vide, deux charges ponctuelles q1 et q2, fixées en M1 et M2. Les deux charges stationnaires q1 et q2 exercent l’une sur l’autre une force proportionnelle à chacune des charges et inversement proportionnelle au carré de la distance qui les sépare. La force électrostatique est dirigée suivant la droite qui joint les charges (figure 1). Elle attractive si les charges sont de signes contraires (figure 1-a), répulsive lorsque les charges sont de même signe (figure 1-b).Conformément au principe de l’action et de la réaction, la force
 exercée par q2 sur la charge q1 est égale et opposée à
exercée par q2 sur la charge q1 est égale et opposée à  :
: 
Les forces
 et
et sont portées par la droite qui joint les charges q1 et q2. C’est une caractéristique que l’on peut expliquer en évoquant le principe d’isotropie : dans un univers vide, aucune direction ne peut être privilégiée par rapport à une autre, toutes les directions sont équivalentes. La présence de deux charges ponctuelles détruit cette isotropie en introduisant une seule direction privilégiée, la droite joignant les charges.
sont portées par la droite qui joint les charges q1 et q2. C’est une caractéristique que l’on peut expliquer en évoquant le principe d’isotropie : dans un univers vide, aucune direction ne peut être privilégiée par rapport à une autre, toutes les directions sont équivalentes. La présence de deux charges ponctuelles détruit cette isotropie en introduisant une seule direction privilégiée, la droite joignant les charges. La constante de proportionnalité est liée aux unités choisies pour exprimer la force, la longueur et la charge. Dans le système d’unités international (S.I.), sous sa forme rationalisée, K s’écrit :
où ε0 est la permittivité du vide et a pour valeur :
3.2 - Validité de la loi de Coulomb
La loi de Coulomb est valable pour des charges au repos où à la limite en mouvement relatif lent. Elle est aussi valable dans le vide et approximativement dans l’air.La loi de Coulomb reste valable pour les très grandes distances dans le domaine microscopique : jusqu’à 10-15 m, ordre de grandeur des dimensions du noyau atomique. Cette loi n’est pas valable pour des distances inférieures à 10-15 m (dimension du noyau atomique).
Dans ce dernier cas, il sera nécessaire d’utiliser la mécanique quantique pour l’étude du comportement des particules sous l’effet des forces coulombiennes.
Dans d’autres milieux linéaires homogènes et isotropes (l.h.i.), l’interaction électrostatique est bien décrite par la loi de Coulomb à condition de remplacer ε0 par une constante ε différente qui tient compte de l’influence du milieu (ses caractéristiques électriques ). ε s’appelle la permittivité diélectrique du milieu et l’on pose dans ce cas εr = ε/ε0 où εr est la permittivité diélectrique relative du milieu (quantité sans dimension).
3.3 - Analogie avec l’interaction de gravitation
Deux points matériels de masse m1 et m2, placées respectivement en M1 et M2 exercent l’un sur l’autre une force de gravitation ; la force exercée par m1 sur m2 est :
exercée par m1 sur m2 est : Où G est la constante de gravitation universelle.
La force de gravitation a la même formulation mathématique que la force électrostatique : elle est portée par la droite qui joint les masses m1 et m2 et inversement proportionnelle au carré de la distance qui sépare les deux masses. Nous verrons au chapitre suivant les propriétés qui découlent de ces deux caractéristiques et qui seront donc applicables aux forces de gravitation. C’est pourquoi on appelle les forces de la forme
 , forces coulombiennes.
, forces coulombiennes. Mais elles sont toujours attractives.
D’après le cours de mécanique du point, la force de gravitation joue un rôle fondamental dans la mécanique des objets macroscopiques et dans la dynamique céleste.
Cependant, à l’échelle atomique et subatomique, la force de gravitation est négligeable.
A titre d’exemple, comparons la force de gravitation qui s’exerce entre l’électron et le proton d’un atome d’hydrogène à la force électrostatique s’exerçant entre eux. La distance r qui sépare l’électron de masse me= 9,1 10-31 kg du proton de masse mp= 1,7 10-27 kg est environ 5 10-11m.
La force électrostatique est 1039 fois supérieure à la force de gravitation. On peut alors s’étonner du fait que dans notre vie quotidienne, nous ne ressentions pas de manifestations de ces forces énormes d’origine électrique. L’existence de deux types de charges de signe contraire, mais de même valeur absolue conduit à des forces de répulsion et d’attraction et la neutralité électrique de la matière assure une compensation entre ces forces. Par contre les forces gravitationnelles bien que d’intensité faible, produisent des effets significatifs car elles sont toujours attractives. On peut imaginer ce qu’entraînerait un léger excès d’électrons sur deux personnes distantes de un mètre : si chacune d’elle porte un pour cent de plus d’électrons que de protons, elles exerceraient entre elles une force capable de soulever la terre toute entière.
4 - PRINCIPE DE SUPERPOSITION
Considérons trois charges ponctuelles q1, q2 et q fixées respectivement en P1, P2 et M (Figure 2).Quelle est la force
 que subit la charge q placée en présence des charges q1 et q2 ?
que subit la charge q placée en présence des charges q1 et q2 ? La loi de Coulomb permet de calculer la force
 subie par la charge q lorsqu’elle est uniquement en présence de q1. On peut de la même manière calculer
subie par la charge q lorsqu’elle est uniquement en présence de q1. On peut de la même manière calculer , force subie par q lorsque seule q2 est en présence de la charge q.
, force subie par q lorsque seule q2 est en présence de la charge q. L’expérience montre que la force
 subit par q lorsqu’elle est en présence des deux charges q1 et q2 est la somme vectorielle des forces
subit par q lorsqu’elle est en présence des deux charges q1 et q2 est la somme vectorielle des forces et
et :
:
Ce résultat est vérifié quel que soit le nombre de charges en présence. La force subie une charge q placée en M, en présence de n chargées q1, q2, ..., qi, ...,qn fixées en P1, P2, ..., Pi, ..., Pn est la somme vectorielle des forces dues à l’interaction de chacune des charges avec q, calculées séparément :
subie une charge q placée en M, en présence de n chargées q1, q2, ..., qi, ...,qn fixées en P1, P2, ..., Pi, ..., Pn est la somme vectorielle des forces dues à l’interaction de chacune des charges avec q, calculées séparément :
 subie une charge q placée en M, en présence de n chargées q1, q2, ..., qi, ...,qn fixées en P1, P2, ..., Pi, ..., Pn est la somme vectorielle des forces dues à l’interaction de chacune des charges avec q, calculées séparément :
subie une charge q placée en M, en présence de n chargées q1, q2, ..., qi, ...,qn fixées en P1, P2, ..., Pi, ..., Pn est la somme vectorielle des forces dues à l’interaction de chacune des charges avec q, calculées séparément :  due à un ensemble de charges est la somme vectorielle de l’effet de chaque charge prise individuellement. Ce qui suppose que la force s’exerçant entre deux charges n’est pas modifiée par la présence d’une troisième charge. Il y a donc indépendance des effets : la solution est simplement la somme des solutions calculées pour chaque couple de charges. Il en résulte que les équations de l’électrostatique sont des équations linéaires. Le principe de superposition s’applique aux phénomènes électromagnétiques : les équations de Maxwell, équations de base de l’électromagnétisme sont des équations linéaires.
due à un ensemble de charges est la somme vectorielle de l’effet de chaque charge prise individuellement. Ce qui suppose que la force s’exerçant entre deux charges n’est pas modifiée par la présence d’une troisième charge. Il y a donc indépendance des effets : la solution est simplement la somme des solutions calculées pour chaque couple de charges. Il en résulte que les équations de l’électrostatique sont des équations linéaires. Le principe de superposition s’applique aux phénomènes électromagnétiques : les équations de Maxwell, équations de base de l’électromagnétisme sont des équations linéaires. Cependant, il ne faut pas en déduire que c’est un principe général en physique. En effet, le principe de superposition ne s’applique pas toujours ; par exemple, dans le domaine atomique ou subatomique, des effets quantiques de nature électromagnétique, non linéaires peuvent apparaître.
5 - LE CHAMP ELECTROSTATIQUE
Considérons la force définie par (4). Divisons l’expression (I-4) par la charge q.
définie par (4). Divisons l’expression (I-4) par la charge q. Nous obtenons une grandeur vectorielle qui dépend de la structure des n charges et de la position du point M : cette grandeur est appelée le champ électrostatique, ) (M E , crée au point M par le système de chargées q1, q2, ..., qi, ..., qn fixées en P1, P2, ..., Pi, ..., Pn.
Le champ électrostatique
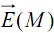 qui résulte de
qui résulte de est la somme vectorielle des champs
est la somme vectorielle des champs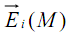 crées par les charges qi :
crées par les charges qi : où
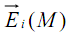 est le champ crée en M par la charge qi ponctuelle placée en Pi (Figure 3)
est le champ crée en M par la charge qi ponctuelle placée en Pi (Figure 3)Nous venons de définir une grandeur vectorielle, fonction du point M, caractéristique du système de charges q1, q2, ..., qi, ...,qn, sources du champ
 . En chaque point de l’espace, on fait correspondre un vecteur
. En chaque point de l’espace, on fait correspondre un vecteur , fonction du point considéré (Figure 3).
, fonction du point considéré (Figure 3). L’ensemble des vecteurs
 constitue un champ de vecteurs. Le champ
constitue un champ de vecteurs. Le champ étant déterminé, la force
étant déterminé, la force que subit une charge q placée en un point M est donnée par la relation :
que subit une charge q placée en un point M est donnée par la relation : L’introduction du champ
 aboutit à une nouvelle description de l’interaction électrostatique. Nous avons remplacée l’action à distance contenue dans la loi de Coulomb par la notion de champ électrostatique, grandeur locale.
aboutit à une nouvelle description de l’interaction électrostatique. Nous avons remplacée l’action à distance contenue dans la loi de Coulomb par la notion de champ électrostatique, grandeur locale. Au lieu de considérer les charges qi et q en présence interagissant par l’intermédiaire de la force de Coulomb :
On exprime le champ
 crée par la charge qi dans tout l’espace entourant cette charge. Ce champ existe indépendamment du fait qu’il existe ou non une autre charge q en présence de la charge qi, source du champ
crée par la charge qi dans tout l’espace entourant cette charge. Ce champ existe indépendamment du fait qu’il existe ou non une autre charge q en présence de la charge qi, source du champ . La force F subie par q placée en M résulte de l’existence en ce point d’un champ électrostatique :
. La force F subie par q placée en M résulte de l’existence en ce point d’un champ électrostatique : I-6 CONCLUSION
Le champ électrostatique crée en un point M par une charge ponctuelle q placée en O est :
Le champ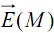 présente deux caractéristiques :
présente deux caractéristiques :
• La première réside dans le fait que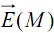 est de la forme
est de la forme , propriété que nous exploiterons dans le calcul de la circulation de E et qui conduira à la définition du potentiel électrostatique.
, propriété que nous exploiterons dans le calcul de la circulation de E et qui conduira à la définition du potentiel électrostatique.
• La deuxième caractéristique est la forme de f(r), en 1/r², propriété que nous exploiterons dans le calcul du flux de et qui conduira au théorème de Gauss. Les résultats que nous
et qui conduira au théorème de Gauss. Les résultats que nous
obtiendrons seront valables pour tout champ de la forme , en particulier le champ de gravitation.
, en particulier le champ de gravitation.
∎ Chapitre II - Champ et potentiel électrostatique
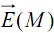 présente deux caractéristiques :
présente deux caractéristiques : • La première réside dans le fait que
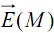 est de la forme
est de la forme , propriété que nous exploiterons dans le calcul de la circulation de E et qui conduira à la définition du potentiel électrostatique.
, propriété que nous exploiterons dans le calcul de la circulation de E et qui conduira à la définition du potentiel électrostatique. • La deuxième caractéristique est la forme de f(r), en 1/r², propriété que nous exploiterons dans le calcul du flux de
 et qui conduira au théorème de Gauss. Les résultats que nous
et qui conduira au théorème de Gauss. Les résultats que nous obtiendrons seront valables pour tout champ de la forme
 , en particulier le champ de gravitation.
, en particulier le champ de gravitation.∎ Chapitre II - Champ et potentiel électrostatique