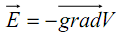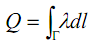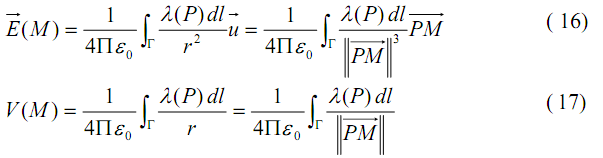Champ et potentiel électrostatique - Cours d’électrostatique



  Champ et potentiel électrostatique

1 - INTRODUCTION

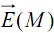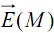Le  potentiel électrostatique V(M) associé au champ  électrostatiqueest une fonction  scalaire contrairement  à  . Nous verrons, dans beaucoup de cas, que le potentiel sera un intermédiaire commode dans le calcul du champ  vectoriel. Le potentiel se rattache physiquement à la notion d’énergie potentielle, d’où son appellation. 

2 - CIRCULATION DU CHAMP ÉLECTROSTATIQUE : LE POTENTIEL ÉLECTROSTATIQUE  

2.1 - Potentiel électrostatique 

a) Cas d’une seule charge ponctuelle

  Considérons une charge ponctuelle q (>0) fixée en P et un point M de l’espace (figure 1) :
 La charge ponctuelle q fixée en P crée  en tout point M de l’espace un champ électrostatique donné par :
vecteur unitaire dirigé de P vers M. 
  La circulation élémentaire dC du champ  E  correspondant à un déplacement élémentaire point M sur la courbe AB est :


La circulation élémentaire dC s’écrit alors :
Posons alors,
V est le potentiel électrostatique V(M) crée par la charge q fixée en M :

   Nous venons de définir un nouveau champ, le  potentiel électrostatique ; c’est un champ scalaire défini à une constante près. On choisit en général la valeur de la constante de telle sorte que le potentiel soit nul lorsque le point M est infiniment éloigné de la charge :
V ( r → ∞)=0  . Dans ce cas, la constante est nulle et le potentiel s’écrit :

 Comme le champ, le potentiel V n’est pas défini aux points Pi :ne sont pas définis.

b) Cas d’une distribution de n charges ponctuelles

Soient n charges ponctuelles q1, q2, ..., qi, ...,qn fixés aux points P1, P2, ..., Pi, ...,Pn. 
Soit M un point de l’espace. (figure 2). 

 Calculons la circulation élémentaire dCi du champcrée par la charge qi seule :
 Ainsi, le potentiel électrostatique Vi(M) dû à la charge qi. 
Le potentiel V(M) dû à l’ensemble des n  charges est la somme des potentiels en application du principe de superposition :
  Dans cette relation, nous avons choisi la constante nulle pour chaque potentiel Vi crée par la charge qi ; ceci n’est pas valable que si les charges qi sont réparties dans un volume fini.

2.2 - Relation entre champ et potentiel électrostatique

  Le potentiel électrostatique a été défini à partir de la circulation élémentaire du champ:
Le  champ électrostatiquedérive du potentiel scalaire V. Par l’intermédiaire de cette relation locale, qui lie le champ électrostatiqueet le potentiel électrostatique V, la connaissance de V en  un point de l’espace  suffit pour la détermination de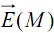. Cette relation implique des conditions de continuité et de dérivabilité sur la fonction V(M).

Unité : l’unité du potentiel électrostatique dans le système MKSA est le Volt (V).
D’après la relation qui lie le  champ électrostatiqueet le potentiel électrostatique V, l’unité du champ électrostatique est le Volt par mètre (V/m).

2.3 - Propriétés 

La circulation CAB du chample long du contour AB est
La circulation du champ de vecteur, le long de AB, est donc égale à la différence de potentiel VA–VB. Ainsi, la connaissance dene définit que les différences de potentiel.
Pour avoir le potentiel en un point, il faudra définir une origine arbitraire des potentiels. Il est commode de choisir le potentiel nul à l’infini quand la distribution de charges est limitée à un domaine fini.
La circulation du champ de vecteur, le long de AB est indépendante de la forme du contour AB ; elle  ne dépend pas du chemin suivi (la circulation élémentaire dC est différentielle totale exacte). 
 En conséquence la circulation deest  nulle le long de tout contour  fermé. Le champest un champ de vecteurs à  circulation conservative qui dérive d’une fonction scalaire appelée potentiel électrostatique. En résumé :


2.4 - Topographie d’un champ électrique

a) Lignes de champ

  Pour avoir une idée sur l’allure du champ, on trace les  lignes de champ, c’est à dire les courbes tangentes en chaque point au vecteur  E  défini en ce point. Ces courbes sont orientées par convention dans le sens du vecteur(figure 3). 
  Soit M un point d’une ligne de champ etle vecteur déplacement élémentaire sur une ligne de champ (Figure 3)
Puisqueetsont colinéaires, on a :
  Cette relation permet d’obtenir les équations des lignes de champ. Dans le système de coordonnées  cartésiennes, posons :
La relation (9) conduit à : 

Exemple de lignes de champ
Soit une charge ponctuelle en O. les lignes du champ crée par la charge ponctuelle sont des demi-droites concourantes en O, divergentes si q > 0 (figure 4-a) et convergentes si q < 0 (figure 4-b).
•  Notons que dans une région où le champest un vecteur bien défini et non nul, on peut suivre de façon continue une ligne de champ 
•  Deux lignes de champ ne peuvent se croiser : la figure 4 montre que les lignes de champ commencent (figure 4-a) ou s’arrêtent (figure 4-b) sur les charges qui sont des points singuliers.

b) Tube de champ

L’ensemble des lignes de champ s’appuyant sur un contour fermé constitue un tube de champ (Figure 5).

c) Surface équipotentielles

Ce sont des surfaces d’équation V = cste, c’est à dire d’égal potentiel (Figure 6). 
D’après la relation, le champest  normal aux surfaces équipotentielles et dirigé vers les potentiels  décroissants (sans le signe moins dans cette relation,est dirigé vers les potentiels croissants).
  Nous avons représenté sur la figure II-6  les surfaces équipotentielles et les lignes du champ  E  crée par une charge ponctuelle positive. Les surfaces équipotentielles sont des sphères centrées en O, point où se trouve la charge. La direction de, c’est à dire du gradient de V est la direction de la normale aux surfaces équipotentielles, celle où V varie le plus rapidement ; il est clair que pour passer de la valeur V1 à la valeur V2, le chemin le plus court est le segment AB. 


Remarque
Lorsqu’on a un système de plusieurs charges, on  ne peut pas obtenir les lignes de champ  par superposition des lignes du champ de chacune des charges. Il faut calculer le champ totalet ensuite tracer les lignes de champ.

2.5 - Signification physique du potentiel électrostatique

  Concéderons une charge q en M soumise à un champ électrostatique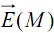due à une certaine distribution de charges discontinue (figure 7).

La force électrostatiqueentraîne un déplacement de la charge q (placée en M) d’un point M1 à un point M2.
La force électrostatique est conservative. Elle dérive donc d’une énergie potentielle U telle que : 
Nous avons introduit la forcepour avoir un moyen d’amener la charge q du point M1 au point M2, qui n’entraîne pas de production d’énergie cinétique. L’opérateur déplace très  lentement la charge q avec une force telle qu’elle équilibre la force électrostatique qui s’applique à la charge :.  Ainsi, un tel déplacement appelé  quasi-statique n’entraîne aucune production d’énergie cinétique. Dans une telle situation, le travail produit en amenant la charge de M1 à M2 se présente sous forme d’énergie potentielle.

 Ainsi, dU représente le travail qu’un opérateur doit appliquer à la charge q contre la force électrostatiquepour déplacer la charge q de dr.
Pour amener la charge du point M1 au point M2, on a :
Le travail de la forcene dépend pas du chemin suivi, il ne dépend que de la position initiale M1 et de la position finale M2. Il s’ensuit que le travail delorsque la charge q est déplacée le long d’un contour fermé est nul, résultat que nous avons obtenu pour la circulation de  E . 
  Exprimons le travailque l’opérateur doit fournir pour amener la charge q de l’infini au point M. Sachant que V(∞)=0  :
 

U(M) est l’énergie potentielle de la charge q placée au point M où le potentiel est V(M), d’où le nom potentiel et la justification du choix du signe moins dans la relation de définition : 
U(M)=qV(M  : énergie potentielle de la charge q placée en un point M où le potentiel est égal à V(M).
L’énergie potentielle est définie à une  constante près. Il en est de même pour le potentiel. Il faut donc un point de référence. Expérimentalement,  seules les différences de potentiel sont accessibles.

3 - DISTRIBUTION CONTINUE DE CHARGES - DENSITE

A l’échelle macroscopique, le nombre de charges élémentaires est si important que la nature discontinue de la charge n’a plus de sens; il en est de même pour la masse puisqu’il ne nous est pas possible de déceler les protons et les électrons à l’échelle macroscopique.
Ceci nous permet de considérer que la répartition de charges dans la matière est continue.  

3.1 - Densité linéique de charge

  Si la charge est concentrée sur un système filiforme, on définit une densité linéique de charges λ(P), à partir de la charge dq porté par un élément dl du fil, entourant le point P :
dq= λdl          (13) 
La charge totale du fil est donnée par l’intégrale curviligne :

3.2 - Densité surfacique de charge


  Lorsque les charges sont  réparties sur une couche d’épaisseur très faible par rapport aux dimensions de la
couche, on définit une densité surfacique de charges σ(P) à partir de la charge dq portée par un élément dS de la surface de la couche, entourant le point P :


dq= σdS      (14)
  Dans ce cas, la charge totale d’une surface (S) est donnée par s’obtient à partir de l’intégrale de surface :

3.3 - Densité volumique de charge


Pour décrire une distribution volumique de charge, on définit la densité volumique de charges ρ(P) à partir de
la charge dq contenue dans un élément de volume dτ entourant le point P :
dq=ρdτ   (15)
  La densité de charges  ρ(P) est une fonction de point  scalaire qui peut subir de grandes variations d’un point à l’autre de la distribution. En effet, la charge est nulle dans l’espace vide entre un noyau et un électron et prend une valeur différente de zéro en un point situé sur le noyau ou l’électron. En conséquence  ρ(P) pourrait avoir des valeurs très différentes suivant le choix du volume élémentaire dτ. Pour que la définition de ρ(P) ait un sens, c’est à dire qu’elle soit indépendante de la forme exacte de dτ, il faut considérer un élément de volume dτ qui soit  grand par rapport aux dimensions atomiques, mais très petit par rapport aux dimensions de la distribution de charges. Celle-ci correspond alors à un système macroscopique et ρ(P) pourra être considéré comme une densité volumique de charges, moyennée sur le volume dτ. Cette description est valable tant que l’on s’intéresse à une description macroscopique (en opposition à microscopique) du système de charges.
Pour un volume τ, la charge totale s’obtient à partir de l’intégrale de volume :


4 - CHAMP ET POTENTIEL D’UNE DISTRIBUTION CONTINUE DE CHARGES 

4.1 - Introduction  

Nous savons déterminer le  champ et le potentiel électrostatique crée par une distribution de charges ponctuelles : 
analogue à l’intégration numérique
  Comment calculer le champ et le potentiel crées par une distribution continue ? La distribution de charges peut être découpée en éléments de volume ou de surface ou de courbe qui portent une charge élémentaire dq. Chacune de ces charges élémentaires crée un champ et un potentiel électrostatiques appelés élémentaires. Le champ (ou le potentiel) crée par toute la distribution est, par application du principe de superposition, la somme des charges (ou des potentiels) élémentaires crées par les charges dq. 

4.2 - Distribution linéique

  On considère une portion de courbe Γ = AB portant une densité linéique de charge λ (figure 8).  
Un élément dl entourant un point P porte une charge : 
Cette charge crée en M un champ et un potentiel donné par les expressions suivantes : 
  D’où le champ total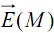et le potentiel V(M) créés en M par toute la distribution linéique de charge s’écrivent : 
Cette dernière relation n’est valable que si le fil est de dimension finie.  
Remarque
On peut montrer que le champ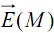et le potentiel V(M) ne sont pas définis en un point M situé sur le fil chargé.  

4.3 - Distribution surfacique

  Dans le cas d’une distribution surfacique  de charges, on considère une charge dq portée par un élément de surface dS (figure 9). 
Le champ et le potentiel crées en M par dq sont donnés par : 
  D’où le champ total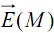et le potentiel V(M) créés par les charges réparties sur la surface Σ : 
Cette relation suppose que la distribution  de charges s’étend sur une surface de dimension fini. Dans le cas contraire, on choisira comme origine des  potentiels un point à distance finie.  

Remarque
On peut montrer que le  potentiel  est défini sur la surface chargée et continue à la traversée de  la surface chargée. Il n’en est pas de même pour le  champqui n’est pas défini sur une surface chargée. Il subit une discontinuité à la traversée de la face chargée.
Nous étudierons le comportement du champà la traversée d’une surface chargée au chapitre III.  

4.4 - Distribution volumique

  Soit une distribution volumique de charges contenue dans le volume v ;  ρ(P) est la densité volumique de charges en un point P du volume v (figure10). 
 
La charge contenue dans l’élément de volume entourant le point P dτP est : 
  Cette charge crée en M un champ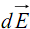et un potentiel dV comme le ferait une charge ponctuelle dq placée en P (Figure 1) : 
  D’après le principe de superposition, le champ total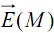créé par la distribution est la somme des contributions:
  Il faut donc calculer une intégrale de volume pour obtenir le champ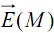alors que le potentiel est obtenu à partir de l’intégrale de volume : 
Cette relation suppose que l’on a choisi le potentiel nul à l’infini, donc que la distribution de charges s’étend sur un volume fini. Si ce n’est pas le cas, il  faut choisir une autre origine des potentiels. 

Remarque
On peut montrer que le  potentiel V et le  champsont définis en un point M intérieur à la distribution de charges.

5 - Conclusion

Le champ électrostatique peut être caractérisé simplement à l’aide d’une fonction que nous appellerons potentiel électrostatique. Cette fonction scalaire est souvent plus simple à déterminer que le champ électrostatique. Cette appellation sera justifiée par l’interprétation de cette fonction en terme d’énergie potentielle  d’une charge soumise aux effets d’un champ électrostatique.

∎ Retour aux plan de cours d’électrostatique

Cours Et Exercices