Calcul direct du potentiel et du champ électrostatique crées par une distribution continue de charges - La solution d'Exercice d'életrostatique

1)  Le point M est sur la médiatrice de AB

Considérons les points A et B sur l’axe x’x  tel que l’origine O soit le milieu de AB (figure 2). Deux éléments de charges dq₁ et dq₂, centrés en deux points P₁ et P₂ symétriques par rapport à O, créent en M des champs électrostatiques élémentaires respectivement et. La résultante de ces champs est portée par la médiatrice (OM), par exemple l’axe y’y de vecteur  j .

 Le champ électrostatiquecréé par l’ensemble de la  charge portée par le segment AB est donc, par raison de symétrie, dirigé suivant l’axe des y. Soit, 

Si on choisit α comme variable d’intégration, on aura : 

Cas limite 
•  Si le point M est très éloigné de l’origine O (a >> L), on a : 

C’est le champ équivalent à celui créé en M par une charge Q= 2λL concentrée en O.
•  Si le point M est très proche du segment (L >> a), on a : 

C’est le champ équivalent à celui créé en M par un fil de longueur infinie uniformément chargé. 

2)  Le point M appartient à (AB)

Un élément de charge dq=λdx centré en P crée en M un champ élémentaire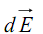porté par   (figure 3) :

Cas limite 
Si le point M est très éloigné du segment [AB] (a >> L), on a :

C’est équivalent du champ créé en M par une charge Q= 2λL  concentrée en O.

∎ Retour Aux Exercices