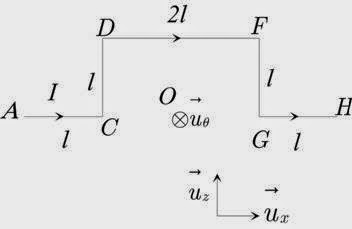
La solution d'Exercice sur Champ magnétique créé par deux circuits de même longueur (Champ magnétique)





On étudie d’abord le premier circuit proposé.
Le plan de la figure est un plan de symétrie de la distribution des courants, au point O le champ
de cette distribution y est donc perpendiculaire. Soit le vecteur unitaire orthogonal à ce plan et orienté vers l’arrière de la figure .

 Les parties horizontales AC et GF  du circuit créent au point O un champ magnétique nul car en chaque point P de ces portions du circuit, l’élément de longueur de ces parties et le vecteur
sont colinéaires.

D’autre part les parties CD et FG créent des champs identiques en ce point O.
En effet pour la partie CD :

Les variables sont liées. On exprime alors l’intégrale uniquement en fonction de la variable On a :angulaire

L’intégration se fera sur l’intervalle car le triangle OCD est isocèle et rectangle en C.
On obtient en remplaçant :

Pour la partie FG on a de même :

Pour la partie DF :



En exprimant les variables x et PO en fonction de la variable angulaire β d’une façon analogue au premier calcul, on obtient :
 Le principe de superposition permet d’exprimer le champ créé en O :

On étudie maintenant le second circuit.

Les portions A’C’ et G’H’ créent en O un champ nul.
La demi-spire a un rayon R tel que d’où : 

La loi de Biot et Savart permet d’écrire que :

Pour avoir l’égalité des deux champs il faut que l’égalité suivante soit vérifiée :

Les courants vérifient alors la relation :









Cours Et Exercices