Combinaisons sans répétition
Supposons maintenant que nous prélevions un échantillon de p éléments de E = { x1, x2,…,xn}. Nous obtenons une partie à p éléments de E.
Définition 1 :
On appelle combinaison sans répétition d’ordre p d’éléments de E toute partie à p éléments de E ;
Proposition 1:
Il y a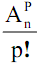
combinaisons d’ordre p de E. noté 
Remarque: Lorsque p > n, un ensemble de cardinal n ne possède pas de parties de cardinal p.
On conviendra donc qu’alors :
.
Les coefficients binomiaux ont un certain nombre de propriétés à connaître.
Proposition 2 :
Exemple 1 :
On doit constituer une équipe de trois ingénieurs et deux techniciens pour s’occuper d’un projet de modernisation d’installations existantes. L’équipe sera constituée à partir du personnel d’un département comportant 9 ingénieurs et 6 techniciens. De combien de manières différentes peut on constituer cette équipe.
Exemple 2 :
Une entreprise comprend 35 employés dont 16 femmes et 19 hommes. On élit le bureau directeur du comité d’entreprise, composé d’un président, d’un vice président, et d’un trésorier. Les postes sont non cumulables.
Quel est le nombre des bureaux possibles
Quel est le nombre des bureaux ?
1) Où le poste de vice président est occupé par une femme ?
2) Où le président et le trésorier sont des hommes?
Définition 1 :
On appelle combinaison sans répétition d’ordre p d’éléments de E toute partie à p éléments de E ;
Proposition 1:
Il y a
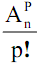combinaisons d’ordre p de E. noté Remarque: Lorsque p > n, un ensemble de cardinal n ne possède pas de parties de cardinal p.
On conviendra donc qu’alors :
. Les coefficients binomiaux ont un certain nombre de propriétés à connaître.
Proposition 2 :
Exemple 1 :
On doit constituer une équipe de trois ingénieurs et deux techniciens pour s’occuper d’un projet de modernisation d’installations existantes. L’équipe sera constituée à partir du personnel d’un département comportant 9 ingénieurs et 6 techniciens. De combien de manières différentes peut on constituer cette équipe.
Exemple 2 :
Une entreprise comprend 35 employés dont 16 femmes et 19 hommes. On élit le bureau directeur du comité d’entreprise, composé d’un président, d’un vice président, et d’un trésorier. Les postes sont non cumulables.
Quel est le nombre des bureaux possibles
Quel est le nombre des bureaux ?
1) Où le poste de vice président est occupé par une femme ?
2) Où le président et le trésorier sont des hommes?