Liaisons entre Solides - Cours de la Mécanique

LIAISONS ENTRE SOLIDES

1 – Définitions

1.1 – Liaison parfaite

Dans un système mécanique, la mise en contact de deux pièces implique des conditions ou des limitations possibles des déplacements relatifs entre ces deux pièces. Le liaison entre deux pièces est donc caractérisée par les surfaces en contact. Pour faire l'étude des différentes liaisons, on fait l'hypothèse de liaison parfaite:

- les surfaces de chacune des pièces sont géométriquement parfaites (pas de défaut de forme ni de rugosité)

- les pièces sont des solides indéformables (pas de déformation ni d'usure)

- pas de jeu entre les pièces

- le contact se fait en un point, une courbe ou une surface de définition géométrique simple (point, droite, cercle, plan, cylindre, sphère).

1.2 – Degrés de liberté d'une liaison

La position d'un solide dans l'espace peut être repérée par 6 paramètres soit 6 mouvements possibles: 3 rotations et 3 translations.

Le nombre de degrés de liberté d'une liaison entre deux solides est le nombre de mouvements indépendants que la liaison autorise.

1.3 – Liaisons normalisées

La norme définit 11 liaisons particulières par leur nom, les degrés de liberté, la représentation schématique (voir tableau). Seules 10 liaisons normalisées sont au programme de prépa.

2 – Chaîne de solides

2.1 – Graphe de structure ou graphe des liaisons

Les solides sont schématisés par des cercles.

Les liaisons sont représentées par des arcs entre les solides.

2.2 – Schéma cinématique

Les pièces sont représentées sans épaisseur avec une couleur par pièce.

Les pièces en liaison fixe (cinématiquement liées) sont représentées de la même couleur.

Les liaisons sont schématisées suivant la norme.

Remarque : on appelle classe d’équivalence un ensemble de solides cinématiquement liés.

Tableau des liaisons normalisées

Désignation	Représentation Plane	Représentation en perspective	Degrés de liberté	Exemples
Encastrement ou liaison fixe			Aucun	Assemblage par vis, goupille, soudure…
Pivot			1 Rz	Roue sur son axe Pivot de porte
Glissière			1 Tz	Tiroir de bureau Assemblage par cannelures ou clavette
Hélicoïdale			1 Rz et Tz liés	Système vis-écrou
Pivot glissant			2 Rz Tz	Arbre à l'intérieur d'un alésage de même diamètre
Appui plan			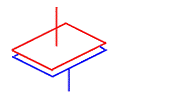3 Ry Tx, Tz	Deux plans en contact
Rotule ou sphérique			3 Rx, Ry, Rz	Contact suivant une portion de sphère
Linéaire rectiligne			4 Ry, Rz Tx, Tz	Contact = droite Cylindre en contact avec un plan selon une génératrice
Linéaire annulaire			4 Rx, Ry, Rz Tz	Sphère dans un cylindre de même diamètre
Ponctuelle			5 Rx, Ry, Rz Tx, Ty	Contact = point Sphère sur plan Surface de faibles dimensions