Déversoir Expérience Manipulation MDF Travaux Pratiques
Introduction :
Le déversoir est un ouvrage
place généralement perpendiculairement a l’écoulement dans un canal le liquide
(eau) s’écoule en formant à l’aval de cet ouvrage une veine libre. Les
déversoirs sont utilises pour régler le courant dans les canaux et permettent
d’en calculer le débit.
Cette
manipulation permettra de tracer les courbes d’étalonnage débit en fonction du
seuil par dessus le déversoir (Q=f(h) ) pour 3 types de déversoirs.
·
un déversoir
rectangulaire a paroi mince et contrainte latérale.
·
deux
déversoirs triangulaires tels que 2a=30° et 2a=90°.
Ces courbes
permettront de mesurer directement un débit dans le canal.
Figure 1 :
déversoir triangulaire et triangulaire
Avec : b = 230 mm.
ASPECTS THEORIQUES :
déversoir
rectangulaire :
le débit Q et la hauteur d’eau h (exprimée en mètre)
au dessus du déversoir sont liés par la relation suivante :
Q = mo´ l(2g)½ h
Le coefficient de débit sans dimensions m est donné
par l’une ou l’autre des formulas empiriques suivantes:
Mo=(0.405+0.003/h)(1+0.55(h/(h+b))²)
1.
BUT :
Le but de cette de manipulation se base sur l’étude
de deux types de déversoirs :
Un déversoir rectangulaire à parois minces et
contraintes latérales.
Deux déversoirs triangulaires telque 2α=90° et
2α=30° cette étude à pour but de vérifier la relation suivante :
Q=C.hα
Après on va s’intéresser à calculer la constante du
débit donnée par l’expression de –Hégaly- dans les différentes cas .
Enfin ,on est amené à tracer les courbe
s
Q=f(h) et ln Q = f(ln h)
PRINCIPE :
Pour
effectuer l’étude précédente on a suivi les étapes suivantes :
·
On place le déversoir sur le banc d’étude.
·
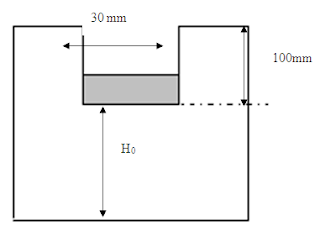
On remplace le banc jusqu’au seuil du déversoir, on
mesure H0 : la hauteur initiale.
·
On actionne la pompe.
Enfin, on
a prélevé une série de mesures du débit et de la hauteur d’eau correspondante
dans le canal en utilisant la vanne.
MANIPULATIONS :
·
Placer le déversoir sur le banc d’étude.
·
Remplir le banc jusqu’au seuil du déversoir à l’aide
d’un compteur volumétrique situé sur la conduite de refoulement, on mesurera le
temps nécessaire à l’écoulement d’un volume donné.
·
Mesurer H et t pour plusieurs débit (au moins 8) entre
le débit maximum (vanne de by-bass totalement fermée) et le débit minimum
(vanne de by-pass totalement ouverte).
Pour
chaque mesure attendre que l’écoulement soit permanent (niveau stabilisé dans
le banc) et refaire la mesure 3 ou 2 fois afin de prendre la valeur moyenne et
l’écart par rapport à celle-ci.
Déversoir triangulaire :
|
|
|
|
|
|
Figure 2 :
déversoir triangulaire à angle 30°
Pour T= 20
°c H0= 45.9 mm V= 2l.
Tableau
de mesure:
Z(mm)
|
t (s)
|
Q(l / s)
|
H =Z - H0
|
-Ln Q
|
-Ln H
|
H1
=98.5
|
T1 =6.32
|
0.34
|
51.63
|
7.98
|
2.96
|
H2
=96.5
|
T2 =5.44
|
||||
H3
= 97.6
|
T3 =5.91
|
||||
H1m = 97.53
|
T1m =5.89
|
||||
H1
=94.5
|
T1=6.56
|
0.3
|
48.43
|
8.11
|
3.02
|
H2
=94.2
|
T2=7.16
|
||||
H3
=94.3
|
T3=6.47
|
||||
H2m =94.33
|
T2m=6.73
|
||||
H1
=90
|
T1=8.37
|
0.24
|
44
|
8.33
|
3.12
|
H2
=89.8
|
T2=8.22
|
||||
H3
=89.9
|
T3=8.18
|
||||
H3m =89.9
|
T3m=8.25
|
||||
H1
=85.9
|
T1=10.37
|
0.19
|
39.76
|
8.56
|
3.22
|
H2
=85.5
|
T2=10.78
|
||||
H3=85.6
|
T3= 10.68
|
||||
H4m=85.66
|
T4m=10.61
|
||||
H1 =83.8
|
T1=12.85
|
0.16
|
37.23
|
8.74
|
3.29
|
H2 =83
|
T2=12.41
|
||||
H3 =82.6
|
T3=12.68
|
||||
H5m=83.13
|
T5m=12.64
|
||||
H1 =82.4
|
T1=13.78
|
0.14
|
36.2
|
8.87
|
3.31
|
H2=81.9
|
T2=14.22
|
||||
H3=82
|
T3=13.47
|
||||
H6m=82.1
|
T6m=13.82
|
La
courbe ln Q = f (lnH)
Détermination
de K et n :
En se
basant sur la courbe on trouve que c’est
une droite qui ne passe pas par l’origine.
Donc :
Ø Ln Q = n lnh + ln K
Avec ln k = cte ; n : la pente.
à ln Q = ln hn + ln K = ln
khn
Alors
Q = k. hn
calcul
de n :
n=tgα = (Δ lnQ) / (Δ lnh)
Ø donc : n
= 2,43393201
Calcul
de k :
Si on
prend ln h = 0 à lnQ = ln K donc ln k c’est
l’intersection de la droite avec l’axe de ln Q donc à partir de la courbe on
trouve que : ln k =0.82
Alors K=
2.1
Déversoir triangulaire :
Ø α/2 = 45 °
H0= 46.1
Z(mm)
|
t (s)
|
Q(l / s)
|
H =Z – H0
|
- Ln Q
|
- Ln H
|
H1
=78.5
|
T1 =4.85
|
0.41
|
32.1
|
7.79
|
3.43
|
H2
=78.1
|
T2 =4.78
|
||||
H3
= 78
|
T3 =4.82
|
||||
H1m =78.2
|
T1m =4.81
|
||||
H1
=70.05
|
T1=7.25
|
0.26
|
23.9
|
8.25
|
3.73
|
H2
=70
|
T2=7.44
|
||||
H3
=70
|
T3=7.85
|
||||
H2m =70
|
7.51
|
||||
H1 =64.7
|
T1=10.91
|
0.19
|
18.13
|
8.56
|
4
|
H2
=64
|
T2=10.16
|
||||
H3
=64
|
T3=9.87
|
||||
H3m =64.23
|
T3m=10.31
|
||||
H1
=62
|
T1=12.67
|
0.16
|
15.85
|
8.74
|
4.14
|
H2
=61.8
|
T2=12.5
|
||||
H3=62.1
|
T3= 12.28
|
||||
H4m=61.95
|
T4m=12.48
|
||||
H1 =61.7
|
T1=2.59
|
0.16
|
15.56
|
8.87
|
4.16
|
H2 61.6
|
T2=12.61
|
||||
H3 =61.7
|
T3=12.22
|
||||
H5m=61.66
|
T5m=12.48
|
La
courbe ln Q = f (lnH)
Détermination
de k et n :
Sur la
courbe on remarque que c’est une droite qui ne passe pas par l’origine
donc :
Ln Q = n ln h + ln K
Avec ln k
= cte ; n = la pente
Ln Q = ln hn
Calcul
de n :
n = tg α = (Δ lnQ) / (Δ lnh) = 1,38733493
Calcul
de k :
Si on
prend ln h = 0 à ln Q
= ln K
donc ln K
c’est l’intersection de la droite avec l’axe des ordonnées ( lnQ).
Donc à
partir de la courbe on trouve que :
Ln K =
3.12
Alors K = 22.64
CONCLUSION :
D’après les résultats obtenus
théoriquement et pratiquement on constate qu’ils sont un peut près égaux. Suivant la relation
Q = k. hn