Régulation proportionnelle

1. Notations et définitions 


M = signal de la mesure
VC = valeur de consigne (en anglais : set point)
e = erreur
e = VC – M   Note : si M > VC, e sera négatif
   si M < VC, e sera positif
m = Signal du régulateur      Δ dans la sortie = final – initial
k = gain (ou coefficient de régulation) 

  Si l’action du contrôleur est basée sur e = VC – M :
   k sera négatif pour une action directe, et
   k sera positif pour une action inverse
b = biais ou valeur de soutien (habituellement 50 % de gamme de sortie)
m = ke + b
↑↑ action directe : M↑ m↑
↑↓ action inverse : M↑ m↓
BP = bande proportionnelle (ou plage de proportionnalité) 
si  BP est étroite, le gain sera élevé
BP est large, le gain sera faible 

2. La régulation proportionnelle en pratique 

On peut réaliser une régulation proportionnelle qui sera plus utile en ajoutant un régulateur entre le transmetteur de niveau et la vanne de régulation. Ce simple ajout permet d’éliminer les difficultés mentionnées
dans le module précédant (lancer le système avec le niveau à sa valeur de consigne) et introduit d’autres avantages que nous exposons dans ce qui suit.  

Dans un système pratique, l’un des problèmes premiers est le mode de défaillance de la vanne. 
Dans notre exemple d’une cuve ouverte dont l’alimentation est commandée par une vanne, il est raisonnable de concevoir le système pour que la vanne se ferme, en cas de panne de l’alimentation en air comprimé, afin d’empêcher le débordement de la cuve. Donc la vanne doit recevoir le signal d’air comprimé pour s’ouvrir.

 Régulation d’une cuve ouverte 

Pour réaliser cette régulation, le système convertir le signal décroissant du transmetteur de niveau en un signal croissant pour la vanne de régulation, par exemple, lors d’une baisse du niveau du liquide dans la cuve. Le régulateur de niveau réalisera cette fonction, appelée action inverse ou indirecte du régulateur et symbolisée par deux flèches pointant en direction opposée (↑↓). Le lecteur voit facilement que si l’on avait opté pour une vanne dont la fermeture est commandée par l’air comprimée, cette inversion n’eût pas été nécessaire. Nous parlerions donc d’une action directe du régulateur, laquelle est symbolisée par deux flèches pointant dans la même direction : (↑↑). Habituellement, on peut utiliser les régulateurs en mode direct ou inverse, en actionnant simplement un commutateur.

Le régulateur acceptera la valeur de consigne et calculera la valeur et la direction de l’écart entre celle-ci et la mesure.  Jusqu’à maintenant, nous avons supposé que le facteur de proportionnalité dût avoir une valeur constante égale à 1, c’est à dire que le signal de régulation était égal à l’erreur mesurée. Or, rien ne prouve que 1 est la meilleure valeur de ce coefficient. Considérons les graphiques suivant qui présentent l’évolution des débits d’entrée, de sortie et du niveau en fonction du temps.    

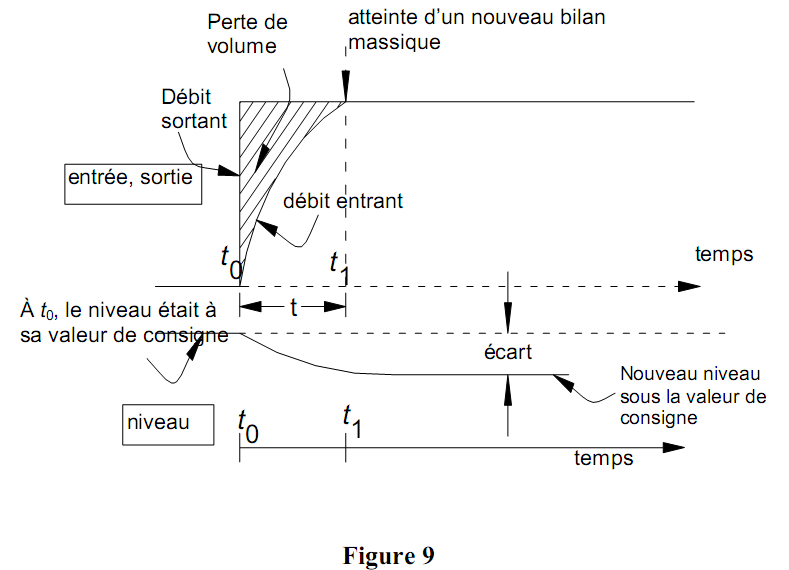
Courbe de réponse à la régulation proportionnelle 

Au temps, t0, la charge (débit sortant) a été augmentée de façon brusque. La correction résultante a conduit à un nouveau bilan massique, au temps t1. À partir de t1, dans ce nouvel équilibre, le niveau sera stabilité sous sa valeur originale (la valeur de consigne) : un écart est apparu qui correspond à une perte de volume correspondant à la zone hachurée entre les courbes des débits d’entrée et de sortie.

 Réponse à la régulation proportionnelle avec une bande
proportionnelle plus étroite 

Considérons de nouveau une perturbation identique de la charge, mais en accroissant cette fois l’ampleur du signal de régulation relativement au signal d’erreur. C’est à dire remplacer l’égalité 
                                          signal de régulation  = signal d'erreur

par  

                                      signal de régulation= gain × signal d'erreur 

Ainsi, comme le montre la figure 9, un signal d’erreur produira un signal de régulation amplifié résultant en un débit d’entrée accru et un temps plus court pour obtenir un nouveau bilan massique. (On peut aussi modifier le « gain » du système de la figure 3.3, où un flotteur actionne une vanne, en déplaçant, sur le levier entre le flotteur et le pivot, le point d’attache de la bielle d’activation de la vanne.) L’écart est très réduit. En instrumentation, on appelle cet ajustement du gain de régulation : la bande proportionnelle
(symbole : BP). .  

La bande proportionnelle est la gamme de variation du signal d’entrée en pourcentage qui causera une variation de 100 % dans le signal de sortie. 
Par exemple, si le signal d’entrée doit varier de 100 % pour changer le signal de sortie de 100 %, le système aura une bande proportionnelle de 100 %. Si, par contre, on modifie le système pour qu’un changement de 50 % dans le signal d’entrée se traduise par une variation de 100 % à la sortie, on aura une bande proportionnelle de 50 %. Il existe une relation évidente entre la bande proportionnelle et le gain. Le gain est défini comme le rapport entre un changement à la sortie et un changement à l’entrée : 

Il est manifeste que si BP = 100 %, le gain sera égal à 1, puisque le changement à la sortie est égal au changement à l’entrée. La bande proportionnelle est l’inverse du gain, exprimé en pourcentage : 

Exemple :
Quel sera le gain d’un régulateur dont la bande proportionnelle est :
a)  de 40 % ?         b)  de 200 % ? 

Réponse :  

Quelle est la bande proportionnelle (en pourcentage) pour les gains
suivants d’un régulateur ?
a) 3   b) 0,4 

Réponse : 

Si la valeur d’une bande proportionnelle (gain élevé) est basse, on parle de bande étroite, alors que si sa valeur est élevée, on parle de bande large. Il n’existe pas de pourcentage canonique permettant de définir les bandes étroites et les bandes larges. On utilise ces notions de façon relative, ainsi une bande proportionnelle de 15 % est plus large qu’une bande de 10 %, alors qu’une bande de 150 % est plus étroite qu’une bande de 200 %. 
Les deux exemples ci-dessus nous ont montré que l’augmentation du gain (ou l’amoindrissement de BP) se traduit par une réduction de l’écart.
Pourrait-on utiliser cette méthode pour le réduire à zéro ? 

Réponses pour différentes valeurs de la bande proportionnelle
(régulation proportionnelle seulement) 

Courbe de la réponse quatre à un 

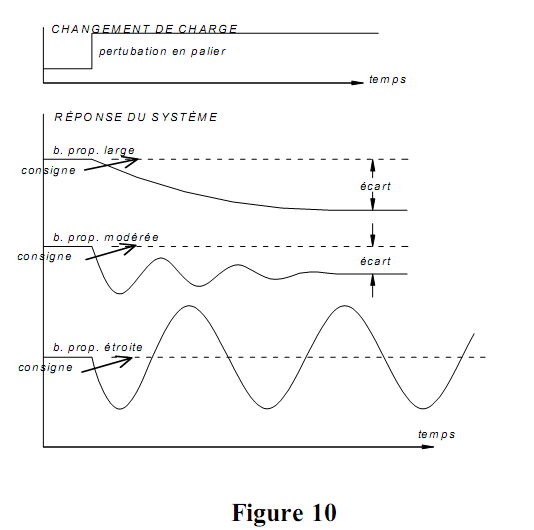
Considérons par exemple un système à gain très élevé, gain = 50 BP = 2 % dont le comportement est illustré à la figure 10. À l’équilibre, lorsque la hauteur du procédé est à la valeur de consigne, le débit entrant sera constant. Ceci signifie habituellement que le signal de régulation d’un régulateur proportionnel sera à 50 %, à la hauteur de consigne. En d’autres mots, nous avons une capacité de régulation de 50 %. Puisque le gain du système est élevé, le signal de régulation maximum sera atteint pour une erreur 1 %, puisque : 

signal de régulation= gain × erreur 

Ce signal de régulation provoquera l’ouverture complète de la vanne, le niveau du liquide montera et dépassera la valeur de consigne. À ce point, le signal d’erreur s’inversera et, lorsqu’il atteindra 1 %, le signal de régulation forcera la fermeture complète de la vanne et donc interrompra le débit entrant. Ce cycle se répétera sans interruption — nous retrouvons la régulation par tout ou rien et tous les avantages qu’elle comporte. Il doit bien exister une valeur optimale de bande proportionnelle offrant un compromis entre un système très stable et paresseux dont les écarts sont important et un système hyperactif, tout ou rien, dont la moyenne de l’écart est zéro. Le réglage considéré optimum qui conduit à l’atténuation (des fluctuations) du système est la méthode de l’atténuation quatre à un, illustrée aux figures 10 et 11.  

On peut voir sur les courbes d’atténuation quatre à un que le procédé retourne à un équilibre après trois cycles d’oscillations amorties. Nous reviendrons sur cette optimisation dans la section sur le réglage du régulateur.  

On se rappellera que le signal de sortie d’un régulateur proportionnel est égal à : 

À l’évidence, si l’erreur est égale à zéro, le signal de régulation sera aussi égal a zéro, une situation qui n’est pas souhaitable. On ajoute donc pour la régulation proportionnelle une valeur constante, ou biais, afin qu’à l’équilibre, le signal de régulation ne soit pas zéro, si l’erreur est nulle. 
Pour les besoins de ce cours, nous supposerons qu’à l’équilibre, si le procédé est à la valeur de consigne, le signal de sortie du régulateur proportionnel sera de 50 %. L’équation de la régulation proportionnelle d’écrit donc : 

Calcul de l’écart :

Exemple :
Soit une cuve dotée d’une vanne pneumatique s’ouvrant sous la pression de l’air. Lorsque le procédé est à sa valeur de consigne, la vanne est ouverte à 50 %. L’augmentation du débit provoque l’augmentation de l’ouverture de la vanne jusqu’à 70 %, valeur qui reste constante. Quel sera l’écart résultat si : 

a)  la bande proportionnelle est de 50 %
b)  la bande proportionnelle est de 25 %
Réponse :
Le régulateur devra être à action inverse (↑↓).
a) Puisque BP = 50 %, gain = 2
  Changement du débit de la vanne = 70 – 50 = 20 %.
  Ce nombre est la variation du signal de sortie du régulateur. 

Puisque le régulateur à une action inverse, la différence sur la grandeur mesurée, Δ ,aura dû être négative : Δ= – 10 %, ce qui équivaut à une erreur positive ou un écart négatif, donc l’écart = – 10 % Il est sous la valeur de consigne.  

b)   Puisque BP = 25 %, gain = 4
Changement du signal, Δentrée = 5 % écart = –5 %, sous la valeur de consigne.
On observera que le choix d’une bande proportionnelle plus étroite se traduira par des oscillations dans le système. On pourra souhaiter que ces oscillations seront amorties. 

3  Points saillants  

•  Pour obtenir l’action régulatrice correcte, on doit opter entre la
réponse directe (↑↑) ou inverse (↑↓) pour le régulateur.
• bande proportionnelle= 100%/gain   ou   gain=100%/BP
•  L’amortissement de quatre à un des oscillations est le réglage
optimal de la bande proportionnelle.