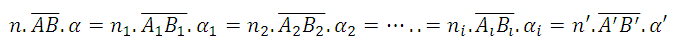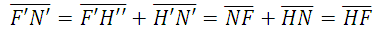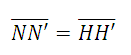Cours d'Optique Géométrique Chapitre 4
►Retour au chapitre 3
►Voir aussi Exercices Corrigés d'otique géométrique
4.1 GÉNÉRALITÉS
4.1.1 DÉFINITION - CONDITIONS DE L’ÉTUDE
Un système centré dioptrique est formé par une succession de surfaces planes ou sphériques séparant des milieux transparents: les centres des faces sont alignés sur un même axe qui constitue l’axe principal du système.
Sauf cas très particulier un tel système ne permet pas de réaliser le stigmatisme rigoureux : on cherche donc le stigmatisme approché en se plaçant dans les conditions de l’approximation de GAUSS.
Si ces conditions sont satisfaites, à un point OBJET correspond un point IMAGE ; un élément d’un plan de front admet une autre portion d’un autre plan de front comme image à travers le système : les deux plans sont des plans conjugués.
4.1.2 CORRESPONDANCE OBJET - IMAGE : RELATION DE LAGRANGE HELMHOLTZ
L’établissement d’une relation de grandeur est immédiat : pour chacun des dioptres constituant le système étudié, lorsque les conditions de l’approximation de GAUSS sont satisfaites, la relation de LAGRANGE / HELMHOLTZ est vérifiée. On a donc:
Ceci établit la relation de LAGRANGE HELMHOLTZ où n et n' sont les indices des milieux respectivement à l’entrée et à la sortie du système centré. AB et A'B' sont les mesures algébriques des dimensions correspondantes de l’objet et de l’image. Enfin α' est l’angle que fait avec l’axe en A' le rayon émergent correspondant à l’incident qui fait l’angle α .
Ce résultat est valable pour tous les couples de points voisins de l’axe des plans de front P et P' passant par K et K' tels que KH = K'H'.
On remarque que le grandissement pour les plans P et P' est égal à 1 : ces deux plans sont donc les plans principaux.
Les points H et H' sont les points principaux. Par définition HH' caractérise l’interstice du système
4.2.4 DISTANCES FOCALES
La distance focale objet est par définition la mesure algébrique HF, parfois notée f = HF. La distance focale image est par définition la mesure algébrique H'F', parfois notée f' = H'F' .
Sur la figure 4 le système est représenté par ses foyers et ses plans principaux : n est l’indice du milieu que voit la face d’entrée et n' l’indice du milieu que voit la face de sortie.
Tous les rayons issus d’un point du plan focal objet émergent parallèles entre eux et donc à K'F'
. Si on applique la relation de LAGRANGE HELMHOLTZ à l’objet HK et à son image H'K', on a :
n.HK .α'.H'K'.a' soit dans ce cas particulier n.α'.a'.
Par ailleurs, dans les conditions de l’approximation de GAUSS :
soit finalement : HF.αH'F'.a'.
En divisant ce résultat par l’égalité n.α'.a', il vient :
a. Soit on trace FJ parallèle à l’incident initial. Au rayon FJ qui est issu du foyer objet F correspond un émergent, parallèle à l’axe, qui coupe le plan focal image en φ'. Par définition du plan focal image, tous les rayons incidents parallèles à FJ convergent au foyer secondaire φ' et par suite l’émergent cherché est K'φ'
b. Soit on considère le foyer secondaire φ'F'. Par suite l’émergent cherché est la parallèle à G'F' passant par K'.
Pour construire les points nodaux à partir des éléments cardinaux déjà connus on procède comme l’indique la figure 9 :
- si φ'F'
. - ceci est vrai pour le rayon incident φ'F' qui coupe l’axe en N.
- l’émergent correspondant à J émerge en J' et son support coupe l’axe en N'.
Sur la figure 7 on voit que les triangles φ'H'F' sont égaux donc :
et on peut trouver de même :
La dernière relation est évidente par application du principe de retour inverse de la lumière (les éléments objets et les éléments images échangent leurs rôles). On peut aussi la démontrer de façon plus lourde après avoir remarqué l’égalité des triangles NHJ et N'H'J' , on a en effet :
Par ailleurs dans le parallélogramme NN'J'J 1es côtés opposés NN' et JJ' sont égaux. Comme de plus JJ'=HH' on en déduit que la distance des points nodaux est égale à l’interstice du système :
Enfin on peut remarquer que :
4.2.7 CONCLUSION - CAS DU DIOPTRE SPHÉRIQUE
Un système centré dioptrique est complètement déterminé par la connaissance de ses éléments cardinaux. Compte tenu des relations qui les tient il suffit de connaître les foyers et les points principaux ou les foyers et les points nodaux.
Le système avec foyers à distance finie le plus simple est le dioptre sphérique. En utilisant les définitions on peut voir que, dans ce cas, les plans principaux sont confondus avec le plan tangent au sommet : H et H' sont en S.
Les points nodaux sont confondus avec le centre C.
On retrouve ces résultats à l’aide de la relation 4.6 : en utilisant les relations 3.2 et 3.3 on a en effet :
4.3 FORMULES DES SYSTÈMES CENTRÉS
4.3.1 FORMULES DE CONJUGAISON
Origines aux points principaux
On repère la position de l’objet A par rapport au point principal objet H à l’aide de HA et la position de l’image A' par rapport au point principal H' à l’aide de H'A' .
Sur la figure10, les triangles LHF et LKB, d’une part, et les triangles K'H'F' et K'L'B' , d’autre part, son semblables. On a donc :
En ajoutant les deux égalités membre à membre il vient :
la relation précédente devient :
En multipliant par :
on fait apparaître la vergence V et la forme la plus utile de la relation de conjugaison :
Origines aux foyers : Formules de NEWTON
On repère la position de l’objet par FA et la position de l’image par F'A'. On voit sur la figure 8 les triangles FAB et FHL, d’une part, F'H'K' et F'A'B', d’autre part, sont semblables. On en déduit :
D’où on tire la relation de conjugaison :
et les expressions du grandissement :
Puisque HF et H'F' sont de signes contraires, il en est de même pour FA et F'A'. Par ailleurs, à chaque valeur du grandissement, correspond une seule position de l’objet.
4.3.2 AUTRES RELATIONS
Comme pour le dioptre sphérique :nG = α'/α est le rapport de convergence et
est le grandissement axial.
De la relation de LAGRANGE HELMHOLTZ, n.AB.α'.A'B'.a'on tire :
Soient A et A' deux points conjugués et AC un petit déplacement de l’objet le long de l’axe. Le déplacement correspondant de l’image est A'C'
.
Si, comme le montre la figure 9, I'C' est le rayon émergent correspondant à l’incident CI, et A'
B' est l’image de AB. On voit que :
d'ou :
Si le déplacement AC est assez petit on peut confondre les valeurs de g, γ , on voit que g =γ2(n'/n) est toujours positif. On peut donc conclure :
POUR LES SYSTÈMES CENTRÉS DIOPTRIQUES L’OBJET ET L’IMAGE SE DEPLACENT
TOUJOURS DANS LE MÊME SENS.
4.3.3 CAS PARTICULIER: MILIEUX EXTRÊMES IDENTIQUES
Ce cas particulier est très important en pratique puisqu’il correspond à tous les systèmes optiques usuels [lentilles, loupes, microscopes (sauf cas du microscope à immersion) lunettes astronomiques, terrestres ... ]dont les faces d’entrée et de sortie baignent dans l’air. Si n = n' on a HF = f = H'F'=f'. On pose alors H'F' et on obtient les résultats suivants où les formules les plus utilisées sont en numérotées. - Formules de conjugaison :
- Grandissement: les relations de NEWTON donnent :
dessus - une nouvelle forme très utile du grandissement :
- Eléments cardinaux : HN = H'N'= HF + H'F'= (-φ)
On cherche à déterminer les éléments cardinaux d’un nouveau système constitué par l’association de deux systèmes dont les éléments cardinaux sont connus. Avec les notations habituelles (H et H', F et F', N et N') on caractérise les éléments du premier système par l’indice 1 et ceux du second système par l’indice 2. Les lettres sans indice désignent des éléments du système complet. n et n' sont les indices des milieux d’entrée et de sortie du système complet ; N est l’indice du milieu qui sépare les deux systèmes. La face d’entrée du système (1) baigne donc dans le milieu d’indice n tandis que sa face de sortie voit le milieu d’indice N. Pour le système (2) c’est le milieu d’indice N qui est en contact avec la face d’entrée tandis que la face de sortie baigne dans le milieu d’indice n'.
La position du second système par rapport au premier est définie si on se donne e = H1H2 qui donne la ”distance” entre le plan principal image du premier système et le plan principal objet du second.
4.4.1 CONSTRUCTION GÉOMÉTRIQUE DES FOYERS ET DES PLANS
PRINCIPAUX
Commenter la construction de l’image
4.4.2 POSITION DES FOYERS
Le foyer image F' de l’ensemble (1) + (2) est l’image du foyer image F1' du système (1) à travers le système (2). Par application de la formule de conjugaison de NEWTON on trouve :
Le foyer objet F de l’ensemble a pour image, à travers le système (1), le foyer objet F2 du système (2). On trouve alors :
Les positions des foyers se déduisent des relations précédentes. N.B. On trouve parfois désignée par le nom de”’ intervalle optique ” la quantité F1'F2 qui caractérise aussi la position du système (2) par rapport au système (1). On a en effet :
4.4.3 CALCUL DES DISTANCES FOCALES
Pour calculer la distance focale image f' on considère, à l’aide de la figure 12a, les égalités résultant de la similitude des triangles :
d'une part
d'une autre part
Puisque H'K' = H1'K1' et H2'G2'=F2Q2 les deux derniers rapports sont égaux et on en déduit :
Un raisonnement analogue à partir de la figure 10b, ou, plus simplement, l’utilisation du principe de retour inverse de la lumière donnent :
4.4.4 FORMULE DE GULLSTRAND
Le nouveau système a pour vergence :
La vergence s’écrit alors :
Dans cette expression on fait alors apparaître les vergences V1 et V2 des deux systèmes :
il vient :
soit finalement, la formule de Gullstrand qui donne la vergence du système complet en fonction des vergences des deux systèmes qui le composent, de l’indice du milieu qui les sépare et de la distance e = H1'H2 :
►Voir aussi Exercices Corrigés d'otique géométrique
SYSTÈMES CENTRÉS DIOPTRIQUES
4.1 GÉNÉRALITÉS
4.1.1 DÉFINITION - CONDITIONS DE L’ÉTUDE
Un système centré dioptrique est formé par une succession de surfaces planes ou sphériques séparant des milieux transparents: les centres des faces sont alignés sur un même axe qui constitue l’axe principal du système.
Sauf cas très particulier un tel système ne permet pas de réaliser le stigmatisme rigoureux : on cherche donc le stigmatisme approché en se plaçant dans les conditions de l’approximation de GAUSS.
Si ces conditions sont satisfaites, à un point OBJET correspond un point IMAGE ; un élément d’un plan de front admet une autre portion d’un autre plan de front comme image à travers le système : les deux plans sont des plans conjugués.
4.1.2 CORRESPONDANCE OBJET - IMAGE : RELATION DE LAGRANGE HELMHOLTZ
L’unicité de la correspondance objet - image se met facilement en évidence dans les conditions de l’approximation de GAUSS :
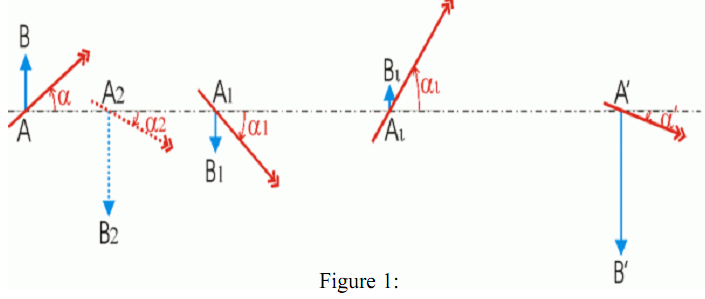
- le dioptre D1 séparant les milieux d’indice n0=n et n1 donne de l’objet A une image A1 qui sert d’objet pour le dioptre D2.
- le dioptre D2 séparant les milieux d’indice n1et n2 donne de l’objet A1 une image A2 qui sert d’objet pour le dioptre D3.
- le dioptre Di séparant les milieux d’indice ni-1 et ni donne de l’objet Ai-1 une image Aii qui sert d’objet pour le dioptre Di+1.
- finalement, le dioptre Dp séparant les milieux d’indice np-1 et np=n' donne de l’objet Ap-1 une image A' qui est unique.
Les rôles de A et A'
peuvent être échangés par application du principe de retour inverse de la lumière. A et A'
sont des points conjugués. Leur correspondance est biunivoque pour un système donné.
Après un choix convenable des origines on pourra donc toujours établir une relation de position biunivoque entre A et A'
.
- le dioptre D1 séparant les milieux d’indice n0=n et n1 donne de l’objet A une image A1 qui sert d’objet pour le dioptre D2.
- le dioptre D2 séparant les milieux d’indice n1et n2 donne de l’objet A1 une image A2 qui sert d’objet pour le dioptre D3.
- le dioptre Di séparant les milieux d’indice ni-1 et ni donne de l’objet Ai-1 une image Aii qui sert d’objet pour le dioptre Di+1.
- finalement, le dioptre Dp séparant les milieux d’indice np-1 et np=n' donne de l’objet Ap-1 une image A' qui est unique.
Les rôles de A et A'
peuvent être échangés par application du principe de retour inverse de la lumière. A et A'
sont des points conjugués. Leur correspondance est biunivoque pour un système donné.
Après un choix convenable des origines on pourra donc toujours établir une relation de position biunivoque entre A et A'
.
4.2 ÉLÉMENTS CARDINAUX
4.2.1 INTÉRÊT DES ÉLÉMENTS CARDINAUX
4.2.1 INTÉRÊT DES ÉLÉMENTS CARDINAUX
Pour certains systèmes centrés simples comme les lentilles, un peut déterminer la position et la dimension de l’image .A'B' d’un objet AB en considérant l’action successive de chacun des dioptres. Mais, plus souvent, on a intérêt à utiliser des points ou des plans possédant des propriétés particulières permettant de construire de façon simple certains rayons réfractés. Ces points et ces plans constituent les éléments cardinaux du système.
Il faut bien remarquer que pour déterminer la position des éléments cardinaux on a besoin de connaître de façon très précise la géométrie (positions des centres et des sommets) et la composition (valeurs des indices des différents milieux) du système. En revanche, une fois ces éléments déterminés, toutes les études ultérieures pourront être effectuées sans avoir à connaître la structure physique du système centré et très simplement en utilisant sa représentation à l’aide de ses éléments cardinaux.
Il faut bien remarquer que pour déterminer la position des éléments cardinaux on a besoin de connaître de façon très précise la géométrie (positions des centres et des sommets) et la composition (valeurs des indices des différents milieux) du système. En revanche, une fois ces éléments déterminés, toutes les études ultérieures pourront être effectuées sans avoir à connaître la structure physique du système centré et très simplement en utilisant sa représentation à l’aide de ses éléments cardinaux.
4.2.2 FOYERS ET PLANS FOCAUX
Par définition, si le point objet est à l’infini sur l’axe, son conjugué est le foyer principal image F'
.
Par définition, le point objet F sur l’axe ayant pour conjugué le point image à l’infini sur l’axe est le foyer principal objet F .
Pour un système, le foyer principal image et le foyer principal objet sont uniques.
.
Par définition, le point objet F sur l’axe ayant pour conjugué le point image à l’infini sur l’axe est le foyer principal objet F .
Pour un système, le foyer principal image et le foyer principal objet sont uniques.
N.B : il convient de bien remarquer que les deux foyers ne sont pas les conjugués l’un de l’autre : l’expérience montre que cette erreur est souvent commise par des étudiants inattentifs.
Le plan focal image et le plan focal objet sont les plans de front correspondants, c’est-à-dire les plans perpendiculaires à l’axe du système respectivement en F' et en F.
Le plan focal image et le plan focal objet sont les plans de front correspondants, c’est-à-dire les plans perpendiculaires à l’axe du système respectivement en F' et en F.
Le plan focal image est le lieu des foyers secondaires où convergent les faisceaux incidents cylindriques. De même le plan focal objet est le lieu des foyers secondaires par où passent les faisceaux émergents cylindriques.
La direction de ces faisceaux cylindriques ne sera déterminée que plus loin 4.2.5.
Si les foyers sont à l’infini le système est dit ” AFOCAL ”. On peut remarquer que le dioptre plan réalise un système afocal.
La direction de ces faisceaux cylindriques ne sera déterminée que plus loin 4.2.5.
Si les foyers sont à l’infini le système est dit ” AFOCAL ”. On peut remarquer que le dioptre plan réalise un système afocal.
4.2.3 PLANS PRINCIPAUX
LES PLANS PRINCIPAUX SONT DEUX PLANS DE FRONT CONJUGUÉS POUR LESQUELS LE GRANDISSEMENT LINÉAIRE EST ÉGAL à 1.
Si, comme sur la figure 3, les foyers F et F' sont à distance finie, on considère un incident SI, parallèle à l’axe, qui émerge suivant I'F'
. On considère également l’incident F J tel que l’émergent correspondant ait même support que SI. Les points de rencontre K des incidents choisis et K' des émergents correspondants existent à distance finie et sont conjugués.
Si, comme sur la figure 3, les foyers F et F' sont à distance finie, on considère un incident SI, parallèle à l’axe, qui émerge suivant I'F'
. On considère également l’incident F J tel que l’émergent correspondant ait même support que SI. Les points de rencontre K des incidents choisis et K' des émergents correspondants existent à distance finie et sont conjugués.
On remarque que le grandissement pour les plans P et P' est égal à 1 : ces deux plans sont donc les plans principaux.
Les points H et H' sont les points principaux. Par définition HH' caractérise l’interstice du système
Propriétés :
C’est le lieu des points d’intersection des incidents parallèles à l’axe et des émergents correspondants passant par F'
C’est le lieu des points d’intersection des incidents parallèles à l’axe et des émergents correspondants passant par F'
4.2.4 DISTANCES FOCALES
La distance focale objet est par définition la mesure algébrique HF, parfois notée f = HF. La distance focale image est par définition la mesure algébrique H'F', parfois notée f' = H'F' .
Sur la figure 4 le système est représenté par ses foyers et ses plans principaux : n est l’indice du milieu que voit la face d’entrée et n' l’indice du milieu que voit la face de sortie.
Tous les rayons issus d’un point du plan focal objet émergent parallèles entre eux et donc à K'F'
. Si on applique la relation de LAGRANGE HELMHOLTZ à l’objet HK et à son image H'K', on a :
n.HK .α'.H'K'.a' soit dans ce cas particulier n.α'.a'.
Par ailleurs, dans les conditions de l’approximation de GAUSS :
soit finalement : HF.αH'F'.a'.
En divisant ce résultat par l’égalité n.α'.a', il vient :
Dans un système dioptrique, les distances focales sont toujours de signes contraires et leur rapport est celui des indices des milieux extrêmes changé de signe.
Comme pour les dioptres on définit la vergence V du système :
Comme pour les dioptres on définit la vergence V du système :
La vergence se mesure en dioptries. Par définition, la dioptrie est la vergence d’un système optique de distance focale 1 mètre dans un milieu d’indice 1.
4.2.5 APPLICATIONS AUX CONSTRUCTIONS GÉOMÉTRIQUES
Construction de l’émergent correspondant à un incident donné
On considère le rayon incident (figures 5 et 6) qui coupe le plan principal objet en K :
l’émergent correspondant passe par le conjugué K' qui appartient au plan principal image: on connaît alors un point du support du rayon émergent et il reste seulement à déterminer sa direction par l’une des deux méthodes décrites ci-après.
l’émergent correspondant passe par le conjugué K' qui appartient au plan principal image: on connaît alors un point du support du rayon émergent et il reste seulement à déterminer sa direction par l’une des deux méthodes décrites ci-après.
a. Soit on trace FJ parallèle à l’incident initial. Au rayon FJ qui est issu du foyer objet F correspond un émergent, parallèle à l’axe, qui coupe le plan focal image en φ'. Par définition du plan focal image, tous les rayons incidents parallèles à FJ convergent au foyer secondaire φ' et par suite l’émergent cherché est K'φ'
b. Soit on considère le foyer secondaire φ'F'. Par suite l’émergent cherché est la parallèle à G'F' passant par K'.
Construction de l’image d’un objet AB
L’aplanétisme étant réalisé dans les conditions de l’approximation de GAUSS, si A est sur l’axe, il suffit de construire l’image du point B. On l’obtient en construisant les émergents correspondants à deux incidents particuliers issus de B :
4.2.6 POINTS NODAUX
LES POINTS NODAUX N ET N’ SONT DEUX POINTS CONJUGUÉS SUR L’AXE TELS QUE TOUT INCIDENT PASSANT PAR N CORRESPOND UN ÉMERGENT PASSANT PAR N’ ET PARALLÈLE A L’INCIDENT.
Pour construire les points nodaux à partir des éléments cardinaux déjà connus on procède comme l’indique la figure 9 :
- si φ'F'
. - ceci est vrai pour le rayon incident φ'F' qui coupe l’axe en N.
- l’émergent correspondant à J émerge en J' et son support coupe l’axe en N'.
Sur la figure 7 on voit que les triangles φ'H'F' sont égaux donc :
et on peut trouver de même :
4.2.7 CONCLUSION - CAS DU DIOPTRE SPHÉRIQUE
Un système centré dioptrique est complètement déterminé par la connaissance de ses éléments cardinaux. Compte tenu des relations qui les tient il suffit de connaître les foyers et les points principaux ou les foyers et les points nodaux.
Le système avec foyers à distance finie le plus simple est le dioptre sphérique. En utilisant les définitions on peut voir que, dans ce cas, les plans principaux sont confondus avec le plan tangent au sommet : H et H' sont en S.
Les points nodaux sont confondus avec le centre C.
On retrouve ces résultats à l’aide de la relation 4.6 : en utilisant les relations 3.2 et 3.3 on a en effet :
4.3 FORMULES DES SYSTÈMES CENTRÉS
4.3.1 FORMULES DE CONJUGAISON
Origines aux points principaux
On repère la position de l’objet A par rapport au point principal objet H à l’aide de HA et la position de l’image A' par rapport au point principal H' à l’aide de H'A' .
Sur la figure10, les triangles LHF et LKB, d’une part, et les triangles K'H'F' et K'L'B' , d’autre part, son semblables. On a donc :
puisque :
la relation précédente devient :
Origines aux foyers : Formules de NEWTON
On repère la position de l’objet par FA et la position de l’image par F'A'. On voit sur la figure 8 les triangles FAB et FHL, d’une part, F'H'K' et F'A'B', d’autre part, sont semblables. On en déduit :
D’où on tire la relation de conjugaison :
4.3.2 AUTRES RELATIONS
Comme pour le dioptre sphérique :nG = α'/α est le rapport de convergence et
De la relation de LAGRANGE HELMHOLTZ, n.AB.α'.A'B'.a'on tire :
Soient A et A' deux points conjugués et AC un petit déplacement de l’objet le long de l’axe. Le déplacement correspondant de l’image est A'C'
.
Si, comme le montre la figure 9, I'C' est le rayon émergent correspondant à l’incident CI, et A'
B' est l’image de AB. On voit que :
POUR LES SYSTÈMES CENTRÉS DIOPTRIQUES L’OBJET ET L’IMAGE SE DEPLACENT
TOUJOURS DANS LE MÊME SENS.
4.3.3 CAS PARTICULIER: MILIEUX EXTRÊMES IDENTIQUES
Ce cas particulier est très important en pratique puisqu’il correspond à tous les systèmes optiques usuels [lentilles, loupes, microscopes (sauf cas du microscope à immersion) lunettes astronomiques, terrestres ... ]dont les faces d’entrée et de sortie baignent dans l’air. Si n = n' on a HF = f = H'F'=f'. On pose alors H'F' et on obtient les résultats suivants où les formules les plus utilisées sont en numérotées. - Formules de conjugaison :
dessus - une nouvelle forme très utile du grandissement :
On cherche à déterminer les éléments cardinaux d’un nouveau système constitué par l’association de deux systèmes dont les éléments cardinaux sont connus. Avec les notations habituelles (H et H', F et F', N et N') on caractérise les éléments du premier système par l’indice 1 et ceux du second système par l’indice 2. Les lettres sans indice désignent des éléments du système complet. n et n' sont les indices des milieux d’entrée et de sortie du système complet ; N est l’indice du milieu qui sépare les deux systèmes. La face d’entrée du système (1) baigne donc dans le milieu d’indice n tandis que sa face de sortie voit le milieu d’indice N. Pour le système (2) c’est le milieu d’indice N qui est en contact avec la face d’entrée tandis que la face de sortie baigne dans le milieu d’indice n'.
La position du second système par rapport au premier est définie si on se donne e = H1H2 qui donne la ”distance” entre le plan principal image du premier système et le plan principal objet du second.
4.4.1 CONSTRUCTION GÉOMÉTRIQUE DES FOYERS ET DES PLANS
PRINCIPAUX
Commenter la construction de l’image
4.4.2 POSITION DES FOYERS
Le foyer image F' de l’ensemble (1) + (2) est l’image du foyer image F1' du système (1) à travers le système (2). Par application de la formule de conjugaison de NEWTON on trouve :
Pour calculer la distance focale image f' on considère, à l’aide de la figure 12a, les égalités résultant de la similitude des triangles :
d'une autre part
Puisque H'K' = H1'K1' et H2'G2'=F2Q2 les deux derniers rapports sont égaux et on en déduit :
Le nouveau système a pour vergence :
il vient :
soit finalement, la formule de Gullstrand qui donne la vergence du système complet en fonction des vergences des deux systèmes qui le composent, de l’indice du milieu qui les sépare et de la distance e = H1'H2 :
