THE ANATOMY OF A MACHINE

EVERY animal is a complex machine, provided with its own motive power and a brain for directing the operation of its own mechanical elements. Not satisfied with the mechanism that nature has put into the human machine, man has reached for other elements and devised mechanisms of his own in order to supplement the human machine and increase its efficiency. At first, as we have seen, these elements were hand tools of the crudest sort; but they were gradually improved and then they were combined into what we term machines. In developing these machines, he naturally took his own system as a pattern and was guided to a large extent by an examination of his own physical structure. We see this very clearly in the names of the different parts of machinery, which are taken from the names of similar parts in the human frame. Almost every member of the body is used in mechanical terminology. For instance, we have the “head” and the “foot,” the “arms” and the “legs,” the “fingers” and the “ankles,” “elbows,” “shoulders,” “trunk,” “hips,” and various parts of the face, such as the “eyes,” “ears,” “nose,” “mouth,” “teeth,” “lips,” and even the “gums,” to indicate parts of machinery which have some remote resemblance to these features.

Before we can understand machinery we must have some general knowledge of the elements of which it is composed. Probably most of the readers of this book already possess a fair knowledge of machine elements and mechanical movements and they can well afford to skip this chapter. However, for the benefit of the uninitiated, we must put a machine on the operating table, dissect it, and explain its anatomical structure. We cannot attempt a very detailed study, but will confine ourselves to the most important elements.
Every machine is made up of movable parts and fixed parts, the latter serving to guide or constrain the motion of the former; for no combination of elements will constitute a machine unless the parts are constrained to move in certain predetermined directions.

THE LEVER

Among the moving elements the first to be considered is the lever, which really forms a broad classification comprising many elements that will hardly be recognized as levers at first blush. Levers in some form are to be found in practically every machine. A wheel, a gear, and a pulley are really levers in disguise, as will be explained presently.
Of course everyone knows that a simple lever consists of a rigid bar that swings on a fulcrum. The fulcrum may be a knife edge, a shaft passing through the bar or any element on which the bar can be swung or oscillated. The purpose of the lever is to give a certain advantage in the application of a force to a load. This may be a change of speed and distance of travel, and hence of power, or merely a change of direction.

FIG. 1.—THREE ORDERS OF SIMPLE LEVERS

There are three types or orders of levers produced by varying the relative positions of the points where the fulcrum, the force or effort, and the weight or load are applied. These are shown in Figure 1. In the lever of the first order the fulcrum is placed between the effort and the weight; in the lever of the second order the weight is applied between the fulcrum and the effort; and in the lever of the third order the effort is applied between the fulcrum and the weight. In each case that part of the lever which extends from the fulcrum to the point where the effort is applied is called the effort arm, and that which extends from the fulcrum to the point where the weight is supported is the weight arm. The weight that can be lifted with a given effort depends upon the ratio of the effort arm to the weight arm. If the two arms are of equal length, the effort is equal to the weight, but twice the weight can be lifted with the same effort if the effort arm is twice as long as the weight arm. You can lift a ton with an effort of only 100 pounds if your effort arm is twenty times as long as your weight arm but the end of your effort arm would have to move twenty inches to raise the ton weight one inch. We are assuming in all these cases that the lever itself has no weight and that there is no friction at the fulcrum.
Of course levers are not used merely for the purpose of lifting weight, but to overcome any resistance or merely to apply pressure upon an object. In almost every household we may find examples of the three orders of levers. A pair of shears, for instance, is composed of two levers of the first order, swinging on a common fulcrum. The effort is applied at the handles, and the weight or load is the material that is cut by the blades or, speaking more technically, the handles are the effort arms and the blades are the weight arms. A material that is too tough to be cut at the tip ends of the blades may be easily cut if we move it in near the fulcrum or pin that hinges the blades together; for by doing this we shorten the weight arms, because the weight arm is measured not to the end of the blade, but to the point where it is cutting into the material. To cut very tough material, such as heavy tin or sheet steel, we use long-handled short-bladed shears. The cutting pressure depends upon the ratio of the effort arm to the weight arm. If the effort arms are twice as long as the weight arms, the cutting pressure is twice as great as that applied at the handles.
A nutcracker consists of a pair of levers of the second order. The fulcrum is at one end and the effort or pressure is applied at the opposite end of the levers or handles, while the equivalent of the weight (in this case the nut) is placed between the effort and the fulcrum. Again the effort arm is[24] measured from the fulcrum or hinge pin of the tool to the point where the hand pressure is applied, and the weight arm is measured from the fulcrum to the nut. The effort arm may be four or five times as long as the weight arm, so that the pressure exerted on the nut is four or five times as great as that exerted by the hand on the ends of the handles.

FIG. 2.—AN ANGULAR OR BELL-CRANK LEVER

In the case of a pair of sugar tongs we have another tool something like the nutcracker in construction, but here the weight, i.e., the lump of sugar, is seized by the ends of the tongs while the hand pressure is applied somewhere between the fulcrum and the weight. Hence we have here a lever or pair of levers of the third order. The effort arm of a pair of tongs is always shorter than the weight arm and the pressure on the sugar lump is always less than that exerted on the tongs by the hand. Evidently the most powerful tool of the three is the nutcracker, because the effort arms extend over the full length of the tool and are always longer than the weight arms.
A lever need not consist of a straight bar; the effort arm may form an angle with the weight arm, forming what is known as an angular or bell-crank lever (Figure 2). When a common claw hammer is used to pull out a nail, the claws that slip under the head of the nail form the weight arm and the hammer handle the effort arm. A horizontal pull on the handle produces a vertical lift on the nail.
Sometimes two or more levers are interconnected, as in Figure 3, the effort arm of one being linked to the weight arm of the other. This serves to increase the lifting force at the weight and at the same time keep the mechanism within compact limits. Such compounding can go on indefinitely and is subject to all sorts of variations.

FIG. 3.—COMPOUND LEVERAGE

One thing we must not forget, and it is a matter that is commonly overlooked by perpetual motion cranks, namely, that while a pound of pressure on the effort arm may be made to lift two, four, or a hundred times as many pounds on the weight arm by varying the relative length of these arms, it has to move two, four, or a hundred times as far as the weight arm, so that the work done on one side of the fulcrum is always exactly equal to that done on the other side.

CONTINUOUS REVOLVING LEVERAGE

FIG. 4.—PRIMITIVE GEAR WHEELS—TWO COACTING GROUPS OF LEVERS

If we take a number of levers radiating from a common fulcrum like the spokes of a carriage wheel, we have a primitive gear wheel. Two such groups of levers may be mounted on parallel shafts so that when one is turned its spokes will successively engage the spokes of the other group and make the latter turn (see Figure 4). Each spoke is first an effort arm on one side of the wheel and then a weight arm as it turns around to the other side of the wheel, and as the effort arms and weight arms are of the same length there is no multiplication of power. A pound on one side of the wheel cannot lift more than a pound on the other. The driven wheel receives the same power as the driving wheel except for such loss as may be due to friction at the bearings or where the spokes contact. The only advantage of such a pair of gears is that the direction of rotation of the driven wheel is the reverse of that of the driving wheel. If the spokes of one wheel are longer than those of the other, we have at once a variation in the rate of rotation proportional to the relative diameters of the two wheels. In Figure 5, for instance, the diameter of the driving wheel A is twice the diameter of the driven gear B, and so, for each revolution of A, B must make two revolutions, i.e., the driver must make two revolutions for each revolution of the driven wheel. In other words, the speed of revolution is doubled. However, if we make B the driver the speed of the driven wheel A will be half of that of wheel B.

FIG. 5.—COACTING LEVERS OF UNEQUAL LENGTH

In primitive machines spoke gears were seldom mounted on parallel shafts because of the difficulty of keeping the spokes in alignment. Instead, one shaft was mounted at right angles to the other so that one set of spokes would cross the other (Figure 6), thus producing the equivalent of a bevel gear. This was of advantage in changing the plane of rotation. A later development was the barrel or lantern gear, which permitted transfer of power without changing the plane of rotation. A cylindrical bundle of rods constituted one of the wheels (as shown in Figure 7). Instead of being crudely formed of spokes, the other wheel sometimes consisted of a disk with pins radiating from its rim. Such gears in far more refined form are still used in modern clocks and watches. A still further development for transmitting motion to a plane at right angles to that of the driving shaft is shown in Figure 8. Here we have a crown gear in which the pins instead of radiating from the periphery of the disk project from the side face of the gear.

FIG. 6.—PRIMITIVE EQUIVALENT OF THE BEVEL GEAR

FIG. 7.—PRIMITIVE LANTERN GEAR

Turning back to our first spoked wheels, it is very evident that we may put a rim over the spokes or even fill in between the spokes and convert the wheels into solid disks that are in frictional engagement with each other without getting away from the fact that we are dealing with levers. Each wheel, then, consists of a continuous revolving lever. Friction gears are used quite commonly in machinery when it is desirable to have the wheels slip if subjected to excessive strain.

TOOTHED GEARS

By forming teeth on one gear to mesh between similar teeth on the other, we convert the friction gears into a pair of spur gears (Figure 9). We need not go into the intricacies of the form of gear teeth. They are designed to be in continuous rolling contact while they are in mesh. The novice is apt to call all spur gears “cogwheels” and gear-teeth “cogs.” Mechanics, however, recognize a difference between cog wheels and spur wheels. In the former, the teeth, or cogs, are not cast upon or cut out of the wheel body, but are separate pieces fitted to the wheel. Such wheels are found in old water mills. They consist of wooden wheels with iron or steel teeth mortised in the wooden rim of the wheel. In general it is safer to speak of spur gears because there are few cogwheels now in use.

FIG. 8.—CROWN AND LANTERN GEAR

When a small gear engages a large one, the former is commonly known as a pinion.

FIG. 9.—SPUR AND PINION GEAR

FIG. 10.—BEVEL FRICTION GEARS

If two friction wheels are to turn at right angles one to the other, they must have conical bearing surfaces, as in Figure 10. The angle between the shafts of the two gears and the relative size of the gears may be changed as desired, provided each cone surface has its apex at the intersection of the two shafts or axes. It is easy to understand how such conical friction gears may be converted into toothed bevel gears (Figure 11), by forming teeth on the conical surfaces, and it will be evident that the teeth must taper toward the apex of the two cones. Two bevel gears of equal diameter, and with shafts set at right angles one to the other, are known as miter gears.

FIG. 11.—TOOTHED BEVEL GEARS

So far we have not shown any combination of gearing that will multiply power. In Figure 5, the driver A is twice the diameter of the driven wheel B, and the latter makes two revolutions for one of A, but the speed at the periphery of the two wheels is the same. A pull of one pound at the point a produces a pressure of one pound at b, and this in turn produces a lift of one pound at c because the levers in each wheel are perfectly balanced, that is, each lever has equal effort and weight arms. The way to obtain an increase of power and of peripheral speed is to fasten two wheels of unequal diameters together on the same center and apply the effort to one of the wheels (as in Figure 12) and the weight to the other wheel. This gives us what is technically known as a wheel and axle. The dotted lines show that we have here a lever of the first order which can be used to multiply power in the same way that a bar lever does. If one wheel is twice the diameter of the other then a pound of effort will lift two pounds of weight.

FIG. 12.—WHEEL AND AXLE OR REVOLVING LEVER OF FIRST ORDER

FIG. 13.—REVOLVING LEVERS OF THE 2D AND 3D ORDER

Figure 13 shows how the effort and weight can be shifted about in such fashion as to give us a lever of the second and one of the third order. The power may be enormously increased and the speed of the final wheel greatly reduced by setting up a train of gears in which the effort is received by the larger one of each couple and is delivered by the smaller one. In Figure 14 the smaller wheels are half the diameter of the larger ones. A pound of pressure at A will amount to 2 at B, 4 at C, 8 at D, 16 at E, and 32 at F. On the other hand, point A will have to move through 32 inches to make the point F move an inch.

RAISING WATER WITH A CHAIN OF POTS

A primitive pump still used in Egypt

A HORSE-OPERATED CHAIN-PUMP USED IN GREECE

MULTIPLE SPINDLE DRILL IN MOTOR CAR FACTORY

FIG. 14.—A TRAIN OF SPUR GEARS

FIG. 15.—PULLEYS OF THE 1ST, 2D, AND 3D ORDERS

FIG. 16.—TYPICAL ARRANGEMENT OF BLOCK AND TACKLE

A pulley is merely a modification of the wheel. Figure 15 shows how it may be arranged to correspond to the three orders of simple levers. If the pulley axis is fixed, as in the first order, the effort and weight arms are equal and hence balanced. In the second order the wheel is bodily movable, hence one pound will raise two pounds of weight because the power arm is twice as long as the weight arm, while in the third order it takes two pounds of lift to raise one pound of weight. There is no end of possible combinations of pulleys which will multiply power in the same way that bar levers do when compounded. A common arrangement of block and tackle is given in Figure 16. There is a four-sheave pulley block above and a three-sheave block below, but in order to trace the rope clearly the pulley wheels or sheaves are represented as of different diameters. The arrangement consists of a series of levers of the first order in the upper pulley block coupled to a series of levers of the second order in the lower block. To find the weight that a given power will lift, multiply the effort by the number of strands of rope that are supporting the weight. In this case there are seven such strands, not counting the strand E, to which the effort or pull is applied. This means that a pull of a hundred pounds at E will lift 700 pounds at W. Of course a pull of seven feet at E will raise the weight only one foot.

FIG. 17.—INCLINED PLANE WITH EFFORT PARALLEL TO THE INCLINED FACE

THE INCLINED PLANE AND ITS FAMILY

The inclined plane constitutes a second broad classification of machine elements. The wedge, the screw, the cam, and the eccentric, all belong to the family of the inclined plane.

FIG. 18.—INCLINED PLANE WITH EFFORT PARALLEL TO THE BASE

A simple form of inclined plane is pictured in Figure 17, which shows a weight W being rolled up an incline. The effort required to carry it to the top of the incline depends, of course, upon the steepness of the incline. The drawing shows a rise of 3 feet on a slope 5 feet long, and the weight of the wheel is, say 20 pounds. To find the effort required, the weight is multiplied by the rise (20 × 3 = 60) and divided by the length of the slope (60/5 = 12) and we find that it takes only 12 pounds to roll the 20-pound wheel to the top of the incline. This holds true when the pull is parallel to the inclined face. If the pull is parallel to the base of the incline, as in Figure 18, we must divide by the length of the base instead of the length of the incline (60/4 = 15) and we find that it takes 15 pounds of effort to pull the weight up the incline. If the pull is exerted at an angle both to the base and the inclined face, we have a problem that is slightly more complicated and we need not go into it here because it involves a bit of trigonometry. In all cases, however, it may be noted that the amount of rope that is taken in, in hauling the weight up the incline, bears a definite relation to the amount of effort required to raise the weight. In Figure 17, 5 feet of rope must be pulled in, in order to raise the weight 3 feet, so that ⅗ of 20 or 12 pounds is all that is required to pull up the weight, while in Figure 18, 4 feet of rope is hauled in for a lift of 3 feet, so that ¾ of 20 or 15 pounds is required to pull up the weight. In this respect the inclined plane is exactly like the lever or the pulley, for the effort multiplied by the distance through which it is exerted is always exactly equal to the weight multiplied by the distance through which it moves. Thus in Figure 17, the effort 12 pounds multiplied by the distance 5 = the weight 20 pounds times the distance 3, and in Figure 18, effort 15 x distance 4 = weight 20 x distance 3. Of course, we are ignoring the weight of the rope and the friction which, in actual practice, are important factors to be reckoned with.

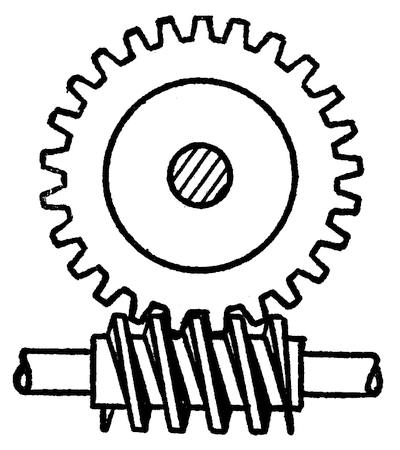
FIG. 19.—ENDLESS SCREW OR WORM GEAR

So far we have considered a fixed inclined plane, but when the inclined plane is moved between the weight and a fixed base it is known as a wedge, and in this case, too, the effort required to move the wedge multiplied by the distance the wedge moves is equal to the weight multiplied by the distance it is lifted.
The commonest form of inclined plane is the screw which is merely an inclined plane bent around a cylinder. A screw engaging a toothed wheel, as in Figure 19, gives a combination known as an “endless screw,” or, more commonly, as a worm gear. The screw or worm is always the driver, and as it must make a complete turn to move the gear through a space of one tooth, the power of this combination is very great. It is practically impossible to turn the worm by using the gear wheel as a driver because the friction developed at the point where the worm and gear contact is very great. For this reason worm gearing is used in the steering gear of automobiles. The shaft of the steering wheel is fitted with a worm which meshes with a worm gear on the parts connected with the wheels. It is very easy to turn the wheels by operating the steering wheel, but if the wheels strike a rut or a stone they are not deflected from their course, because the worm makes it impossible for them to turn the steering wheel.

FIG. 20.—HELICAL OR SPIRAL GEARS

The spiral gear shown in Figure 20 is a cross between a worm gear and spur gear. The teeth are spirals set at an angle of 45 degrees to the axis of the wheel. In this case either gear can be used to drive the other, and the advantage of such a pair is that power is transmitted from one shaft to another in a different plane and at right angles to the first.

FIG. 21.—DRUM CAM

FIG. 22.—PROFILE OR DISK CAM

Cams are usually irregular revolving inclined planes. Figure 21, shows a cylinder or drum cam. A groove is cut in the cylindrical wall of the cam and an arm or lever is provided with a roller which rolls in the groove. When the cam is revolved the lever is constrained to follow all the twists and turns of the groove. A different form of cam is shown in Figure 22. It is formed with an irregular periphery against which the roller is pressed by a spring. As the cam wheel revolves, the roller and the arm to which it is attached must move in and out over all the hills and valleys of the periphery. The cam is one of the most useful elements in modern machinery, for it provides a very simple means of producing the most complicated and irregular motions.

FIG. 23.—ECCENTRIC BY WHICH ROTARY MOTION IS CONVERTED INTO RECTILINEAR MOTION

We cannot attempt to describe all the different types of cams, but reference should be made to the eccentric, which is a form of cam commonly used to operate the valves of a steam engine. The cam in this case is a perfectly circular disk, but the shaft that turns it does not lie at the center of the disk, consequently an object bearing against the periphery must move toward and away from the center as the disk revolves. Instead of using a spring-pressed roller to bear against one side of the disk, the whole disk is encircled with a ring of steel known as an eccentric strap. This strap is bolted to a valve rod and as the eccentric revolves the strap makes the valve rod move back and forth. (See Figure 23.)
A description of all the various combinations of gearing, link motions, ratchets, escapements, clutches, and miscellaneous movements would easily fill the rest of this book, and we must therefore content ourselves with this very brief survey of a few of the more important elements employed in the construction of modern machinery.