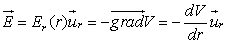La solution d'Exercice sur Théorème de Gauss Atome d'hydrogène.
Atome d'hydrogène.
1. Champ électrostatique.
Comme
le vecteur champ électrostatique est l'opposé du
gradient du potentiel V et qu'il ne
dépend que r (la distribution étant à
symétrie sphérique) on obtient :
2. Flux du champ.
Le
flux du champ électrostatique est défini par :
Comme
la composante du champ est radiale et constante sur
une sphère de rayon r :
L'étude des limites donne :
Φ =
0
pour r tendant vers l'infini.
D'après le théorème de Gauss, la charge intérieure à
une sphère de rayon r à pour expression :
On
peut donc conclure que la charge totale de la
distribution est nulle et qu'au point O on a
une charge ponctuelle positive q.
3. Densité volumique de
charge.
La
charge contenue entre les sphères de centre O et de
rayon r et r + dr est:
On
obtient alors :
Cette
densité de charges est négative et a une charge
totale -q.
4. Fonction
La
fonction étudiée est la densité radiale de charges
et passe par un extremum en r = a.
5. Atome d'hydrogène.
La
distance a est le rayon de Bohr qui est la
distance au noyau pour laquelle la probabilité de
présence de l'électron est maximale.